题目内容
如图,点I是△ABC的内心,AI交BC边于D,交△ABC的外接圆于点E.
求证:(1)IE=BE;
(2)IE是AE和DE的比例中项.
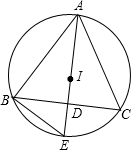
求证:(1)IE=BE;
(2)IE是AE和DE的比例中项.

证明:(1)连接BI,
∵I是△ABC的内心,
∴∠1=∠2,∠3=∠4,
∵∠BIE=∠1+∠3,
∠IBE=∠5+∠4,
而∠5=∠1=∠2,
∴∠BIE=∠IBE,
∴IE=BE.
(2)根据(1)可得:
∵∠2=∠1=∠5,∠E=∠E,
∴△AEB∽△BED,
∴
=
,
∵BE=IE,
∴
=
,
∴IE是AE和DE的比例中项.
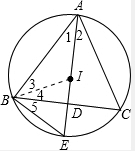
∵I是△ABC的内心,
∴∠1=∠2,∠3=∠4,
∵∠BIE=∠1+∠3,
∠IBE=∠5+∠4,
而∠5=∠1=∠2,
∴∠BIE=∠IBE,
∴IE=BE.
(2)根据(1)可得:
∵∠2=∠1=∠5,∠E=∠E,
∴△AEB∽△BED,
∴
| AE |
| BE |
| BE |
| DE |
∵BE=IE,
∴
| AE |
| IE |
| IE |
| DE |
∴IE是AE和DE的比例中项.


练习册系列答案
相关题目
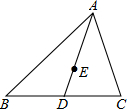
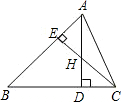
 以1.5厘米∕秒的速度移动,点Q从点B开始沿BC边向C点以2厘米∕秒的速度移动.
以1.5厘米∕秒的速度移动,点Q从点B开始沿BC边向C点以2厘米∕秒的速度移动.