��Ŀ����
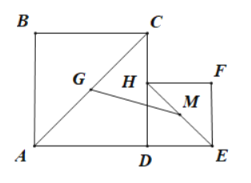
����Ŀ����ͼ������ABCD�У�AB=8��BC=12��E��BC�ߵ��е㣬��P���߶�AD�ϣ���P��PF��AE��F����PA=x��
��1����֤����PFA�ס�ABE��
��2������P���߶�AD���˶�ʱ���Ƿ����ʵ��x��ʹ���Ե�P��F��EΪ�����������Ҳ���ABE���ƣ������ڣ������x��ֵ���������ڣ���˵�����ɣ�
��3��̽��������DΪԲ�ģ�DPΪ�뾶�ġ�D���߶�AEֻ��һ��������ʱ����ֱ��д��DP������������� ����
���𰸡���1������������2�����ڣ�����������x��ֵΪ6��![]() ����3��DP=
����3��DP=![]() ��10��DP��12
��10��DP��12
��������
��1�����ݾ��ε����ʣ������֪��������֤�������Ƕ�Ӧ��ȣ��Ӷ�֤�����������ƣ�
��2�����ڶ�Ӧ��ϵ��ȷ��������Ӧ��Բ�ͬ�Ķ�Ӧ��ϵ��������ǣ�������PEF=��EABʱ����õ��ı���ABEPΪ���Σ��Ӷ����x��ֵ��������PEF=��AEBʱ���ٽ�ϣ�1���еĽ��ۣ��õ�������APE���ٸ��ݵ��������ε����ߺ�һ�õ�F��AE���е㣬���ù��ɶ��������������ε����ʽ�����⣮
��3�����ȼ���ԲD���߶�����ʱ��x��ֵ���ڻ���ԲD��Eʱ���뾶r��ֵ��ȷ��x��ֵ���뾶����ʱ��ʱ�������⣬����ͼ��ȷ��x��ȡֵ��Χ,�Ӷ��ó�DP�ķ�Χ��
��1��֤����������ABCD��
���ABE=90����AD��BC��
���PAF=��AEB��
����PF��AE��
���PFA=90��=��ABE��
���PFA�ס�ABE��
��2���⣺�ֶ��������
������EFP�ס�ABE����ͼ1��
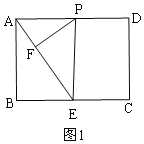
����PEF=��EAB��
��PE��AB��
���ı���ABEPΪ���Σ�
��PA=EB=6����x=6��
����ͼ2������PFE�ס�ABE��

����PEF=��AEB��
��AD��BC
���PAF=��AEB��
���PEF=��PAF��
��PE=PA��
��PF��AE��
����FΪAE���е㣬
Rt��ABE��AB=8��BE=6��
��AE=![]() =
=![]() =10��
=10��
��EF=![]() ��
��
�ߡ�PFE�ס�ABE��
��![]() ��
��
��![]() ��
��
��PE=![]() ��
��
������������x��ֵΪ6��![]() ��
��
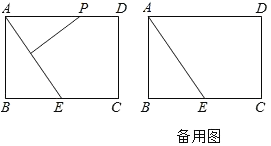
��3����ͼ3������D��AE����ʱ�����е�ΪG������DG��
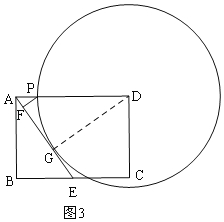
��AP=x��
��PD�TDG=12��x��
�ߡ�DAG=��AEB����AGD=��B=90����
���AGD�ס�EBA��
��![]() ��
��
��![]() ��
��
��x=![]() ��
��
��![]() ��
��
����D����Eʱ����ͼ4����D���߶������������㣬����DE��
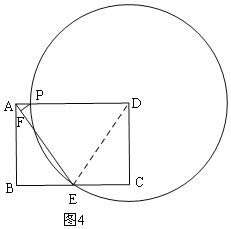
��ʱPD=DE=10��
�ʴ�Ϊ��DP=![]() ��10��DP��12��
��10��DP��12��