题目内容
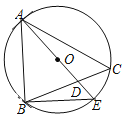
【题目】如图,在△ABC中,已知∠ACB=90°,∠A=30°,BC=6,D为斜边AB上一点,以CD、CB为边作平行四边形CDEB,当AD=_____时,平行四边形CDEB为菱形.

【答案】6
【解析】
连接CE交AB于点O,首先根据含30°角直角三角形的性质得AB=12,由菱形的性质可得OD=OB,CD=CB,由三角形面积可求出OC,根据勾股定理可得OB,由AD=AB﹣2OB即可求AD的长.
解:连接CE交AB于点O,如图所示:
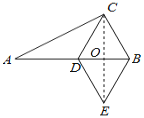
∵Rt△ABC中,∠ACB=90°,∠A=30°,BC=6,
∴AB=2BC=12,AC=![]() ,
,
当平行四边形CDEB为菱形时,CE⊥BD,OD=OB,CD=CB,
∵![]() ABOC=
ABOC=![]() ACBC,
ACBC,
∴OC=![]() ,
,
∴OB=![]() ,
,
∴AD=AB﹣2OB=12﹣2×3=6,
故答案为:6.

练习册系列答案
相关题目