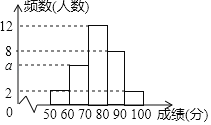
题目内容
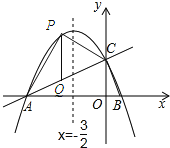
【题目】如图,在平面直角坐标系xOy中,直线y=![]() x+2与x轴交于点A,与y轴交于点C.抛物线y=ax2+bx+c的对称轴是x=﹣
x+2与x轴交于点A,与y轴交于点C.抛物线y=ax2+bx+c的对称轴是x=﹣![]() 且经过A、C两点,与x轴的另一交点为点B.
且经过A、C两点,与x轴的另一交点为点B.
(1)①直接写出点B的坐标;②求抛物线解析式.
(2)若点P为直线AC上方的抛物线上的一点,连接PA,PC.求△PAC的面积的最大值,并求出此时点P的坐标.
(3)抛物线上有一点M,过点M作MN垂直x轴于点N,使得以点A、M、N为顶点的三角形与△ABC相似,直接写出点M的坐标.
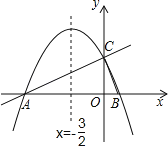
【答案】(1)①B(1,0);②y=![]() x2
x2![]() x+2;(2)△PAC的面积有最大值是4,P(﹣2,3);(3)M1(0,2),M2(﹣3,2),M3(2,﹣3),M4(5,﹣18)
x+2;(2)△PAC的面积有最大值是4,P(﹣2,3);(3)M1(0,2),M2(﹣3,2),M3(2,﹣3),M4(5,﹣18)
【解析】
(1)①先根据直线的解析式求出A,C的坐标,再利用抛物线的对称轴即可求出点B的坐标;
②将抛物线的解析式设成两点式,然后利用待定系数法即可求解;
(2)过点P作PQ⊥x轴交AC于点Q,设![]() ,则Q(m,
,则Q(m,![]() m+2),表示出PQ,然后利用
m+2),表示出PQ,然后利用![]() 求解即可;
求解即可;
(3)以点A、M、N为顶点的三角形与△ABC相似,则有![]() 或
或![]() ,设
,设![]() ,则
,则![]() ,分别利用勾股定理求出AC,BC的长度,然后建立关于t的方程求解即可.
,分别利用勾股定理求出AC,BC的长度,然后建立关于t的方程求解即可.
解:(1)①令![]() ,则
,则![]() ,解得
,解得![]() ,令
,令![]() ,则
,则![]() ,
,
∴![]() .
.
∵抛物线的对称轴为![]() ,
,
![]() ,
,
![]() ;
;
②∵抛物线y=ax2+bx+c过A(﹣4,0),B(1,0),
∴可设抛物线解析式为y=a(x+4)(x﹣1).
又∵抛物线过点C(0,2),
∴2=﹣4a
∴a=![]()
∴y=![]() x2
x2![]() x+2.
x+2.
(2)过点P作PQ⊥x轴交AC于点Q,
设![]() ,则Q(m,
,则Q(m,![]() m+2),
m+2),
![]()
![]()
∴当m=﹣2时,△PAC的面积有最大值是4.
当m=﹣2时,![]() ,
,
∴此时P(﹣2,3).
(3)![]()
∴以点A、M、N为顶点的三角形与△ABC相似,则有![]() 或
或![]()
∵![]()
![]()
设![]() ,则
,则![]()
若![]() ,则
,则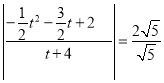
解得![]() 或
或![]() ,
,
此时M的坐标为![]() 或
或![]() ;
;
若![]() ,则
,则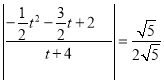
解得![]() 或
或![]() ,
,
此时M的坐标为![]() 或
或![]() ;
;
综上所述,M的坐标为M1(0,2),M2(﹣3,2),M3(2,﹣3),M4(5,﹣18).

 备战中考寒假系列答案
备战中考寒假系列答案【题目】某乒乓球馆使用发球机进行辅助训练,出球口在桌面中线端点A处的正上方,假设每次发出的乒乓球的运动路线固定不变,且落在中线上,在乒乓球运行时,设乒乓球与端点A的水平距离为x(米),与桌面的高度为y(米),经多次测试后,得到如下部分数据:
x/米 | 0 | 0.2 | 0.4 | 0.6 | 1 | 1.4 | 1.6 | 1.8 | … |
y/米 | 0.24 | 0.33 | 0.4 | 0.45 | 0.49 | 0.45 | 0.4 | 0.33 | … |
(1)由表中的数据及函数学习经验,求出y关于x的函数解析式;
(2)试求出当乒乓球落在桌面时,其落点与端点A的水平距离是多少米?
(3)当乒乓球落在桌面上弹起后,y与x之间满足![]() .
.
①用含a的代数式表示k;
②已知球网高度为0.14米,球桌长(1.4×2)米.若a=-0.5,那么乒乓球弹起后,是否有机会在某个击球点可以将球沿直线扣杀到端点A?请说明理由.