题目内容
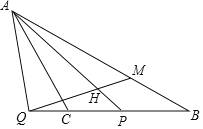
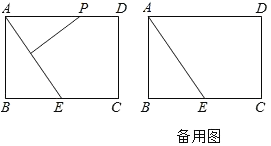
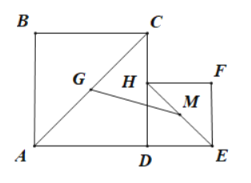
【题目】如图,已知![]() ,点
,点![]() 为
为![]() 上的一点,在
上的一点,在![]() 同侧作正方形
同侧作正方形![]() ,正方形
,正方形![]() 分别为对角线
分别为对角线![]() 的中点,连结
的中点,连结![]() 当点
当点![]() 沿着线段
沿着线段![]() 由点
由点![]() 向点
向点![]() 方向上移动时,四边形
方向上移动时,四边形![]() 的面积变化情况为( )
的面积变化情况为( )
A.不变B.先减小后增大
C.先增大后减小D.一直减小
【答案】B
【解析】
连接DG、DM,把四边形面积分成三个三角形面积,设AD=x,则DE=10-x,则这三个三角形的面积均可用x表示出来,根据所得的函数式分析其变化规律.
解:连接DG、DM. 设AD=x,则DE=10-x,
∵四边形ABCD和四边形DEFH都是正方形,且G、M为对角线的中点,
∴△ADG和△DME都是等腰直角三角形.
∴DG=![]() DM=
DM=![]()
∴四边形AGME的面积=△ADG面积+△DME面积+△GDM面积
=![]()
=![]()
这是一个开口向上,对称轴是直线![]() 的抛物线,
的抛物线,
当![]() 时,面积有最小值.
时,面积有最小值.
所以其面积变化是先减小后增大,
故选:B

练习册系列答案
相关题目