题目内容
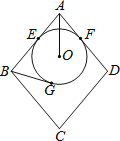
【题目】⊙O是△ABC的外接圆，AB是直径，过 
的中点P作⊙O的直径PG，与弦BC相交于点D，连接AG、CP、PB．
（1）如图1，求证：AG=CP； 
（2）如图2，过点P作AB的垂线，垂足为点H，连接DH，求证：DH∥AG； 
（3）如图3，连接PA，延长HD分别与PA、PC相交于点K、F，已知FK=2，△ODH的面积为2 
，求AC的长． 
【答案】
（1）证明：∵过 
的中点P作⊙O的直径PG，
∴CP=PB，
∵AB，PG是相交的直径，
∴AG=PB，
∴AG=CP
（2）证明：如图 2，连接BG
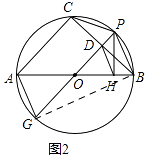
∵AB、PG都是⊙O的直径，
∴四边形AGBP是矩形，
∴AG∥PB，AG=PB，
∵P是弧BC的中点，
∴PC=BC=AG，
∴弧AG=弧CP，
∴∠APG=∠CAP，
∴AC∥PG，
∴PG⊥BC，
∵PH⊥AB，
∴∠BOD=90°=∠POH，
在△BOD和△POH中，
，
∴△BOD≌△POH，
∴OD=OH，
∴∠ODH= 
（180°﹣∠BOP）=∠OPB，
∴DH∥PB∥AG
（3）解：如图3，作CM⊥AP于M，ON⊥DH于N，
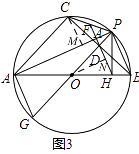
∴∠HON= ∠BOP= ∠COP=∠CAP，
∴△HON∽△CAM，
∴ 
，
作PQ⊥AC于Q，
∴四边形CDPQ是矩形，
△APH与△APQ关于AP对称，
∴HQ⊥AP，
由（1）有：HK⊥AP，
∴点K在HQ上，
∴CK=PK，
∴PK是△CMP的中位线，
∴CM=2FK=4，MF=PF，
∵CM⊥AP，HK⊥AP，
∴CM∥HK，
∴∠BCM+∠CDH=180°，
∵∠BCM=∠CAP=∠BAP=∠PHK=∠MHK，
∴∠MHK+∠CDH=180°，
∴四边形CDHM是平行四边形，
∴DH=CM=4，DN=HN=2，
∵S△ODH= DH×ON= ×4×ON=2 
，
∴ON= ，
∴OH= 
=5，
∴AC= 
=10
【解析】（1）利用等弧所对的圆周角相等即可求解；（2）利用等弧所对的圆周角相等，得到角相等∠APG=∠CAP，判断出△BOD≌△POH，再得到角相等，从而判断出线平行；（3）由三角形相似，得出比例式，△HON∽△CAM， ，再判断出四边形CDHM是平行四边形，最后经过计算即可求解．
