Question

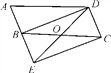
【题目】如图，已知△ABC和△ECD都是等边三角形，B、C、D在一条直线上。

求证：（1）BE=AD;

(2) △FCH是等边三角形

（3）求∠EMD的度数。

Answer 1

【答案】（1）见解析；（2）见解析；（3）∠EMD=60.

【解析】分析: (1)证明△BCE≌△ACD,再根据全等三角形的性质可得AD=BE; (2)根据全等三角形的性质可得∠BEC=∠ADC,然后根据三角形内角和定理可得∠EMH==∠HCD,进而可得答案.

详解: （1）∵△ABC和△DEC是等边三角形,

∴AC=BC,CE=CD,∠ACB=∠ECD=60°,

∴∠ACB+∠ACE=∠ECD+∠ACE,

∴∠BCE=∠ACD,

在△BCE和△ACD中,

AC=BC,∠BCE＝∠ACD,CE＝CD，

∴△BCE≌△ACD（SAS）,

∴AD=BE．

（2）∵△BCE≌△ACD,

∴∠BCE=∠ADC．

∵∠FCE=∠HCD=60°,

在△FCE和△HCD中,

∠BCE=∠ADC,CE =CD,∠FCE=∠HCD,

∴△BCE≌△ACD （ASA）,

∴CF =CH.

在△CFH中,

∵ CF=CH , ∠FCH=60°,

∴△FCH是等边三角形

(3) ∵ △BCE≌△ACD,

∴∠BEC =∠ADC.

在△MHE和△CHD中,

∵∠MEH =∠CDH,

∠MHE =∠CHD（对顶角相等）,

∴∠EMH =∠HCD=60°,

∴∠EMD=60.