题目内容
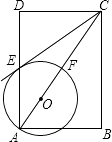
【题目】如图,矩形ABCD的对角线AC,BD相交于点O,点E,F在BD上,BE=DF.
(1)求证:AE=CF;
(2)若AB=6,∠COD=60°,求矩形ABCD的面积.

【答案】![]()
【解析】试题分析:(1)由矩形的性质得出OA=OC,OB=OD,AC=BD,∠ABC=90°,证出OE=OF,由SAS证明△AOE≌△COF,即可得出AE=CF;
(2)证出△AOB是等边三角形,得出OA=AB=6,AC=2OA=12,在Rt△ABC中,由勾股定理求出BC的长,即可得出矩形ABCD的面积.
试题解析:(1)证明:∵四边形ABCD是矩形,∴OA=OC,OB=OD,AC=BD,∠ABC=90°,∵BE=DF,∴OE=OF,在△AOE和△COF中,∵OA=OC,∠AOE=∠COF,OE=OF,∴△AOE≌△COF(SAS),∴AE=CF;
(2)解:∵OA=OC,OB=OD,AC=BD,∴OA=OB,∵∠AOB=∠COD=60°,∴△AOB是等边三角形,∴OA=AB=6,∴AC=2OA=12,在Rt△ABC中,BC=![]() =
=![]() ,∴矩形ABCD的面积=ABBC=6×
,∴矩形ABCD的面积=ABBC=6×![]() =
=![]() .
.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目