题目内容
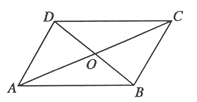
【题目】如图，四边形ABCD中，AC，BD相交于点O，O是AC的中点，AD//BC，AC=8,BD=6.
（1）求证：四边形ABCD是平行四边形；
（2）若AC⊥BD，求□ABCD的面积.
【答案】（1）证明见解析；（2）24.
【解析】试题分析：(1)先证明△AOD≌△COB，可证明对角线互相平分，从而证明平行四边形.(2)由题意得四边形是菱形，菱形的面积等于对角线积的一半.
试题解析：
解：(1)证明：∵O是AC的中点，∴OA＝OC.
∵AD∥BC，∴∠DAO＝∠BCO.又∵∠AOD＝∠COB，
∴△AOD≌△COB，
∴OD＝OB，
∴四边形ABCD是平行四边形．
(2)∵四边形ABCD是平行四边形，AC⊥BD，∴四边形ABCD是菱形，∴ABCD的面积＝
AC·BD＝24.
练习册系列答案
相关题目
