ЬтФПФкШн
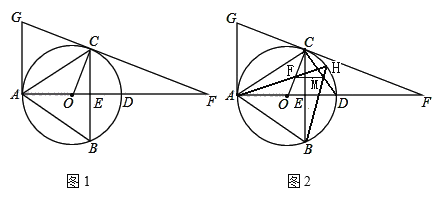
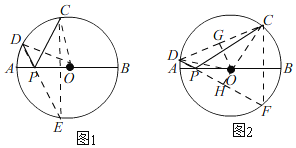
ЁОЬтФПЁПШчЭМЃЌЁбOЕФжБОЖABЃН26ЃЌPЪЧABЩЯ(ВЛгыЕуAЁЂBжиКЯ)ЕФШЮвЛЕуЃЌЕуCЁЂDЮЊЁбOЩЯЕФСНЕуЃЌШєЁЯAPDЃНЁЯBPCЃЌдђГЦЁЯCPDЮЊжБОЖABЕФЁАЛиа§НЧЁБЃЎ
(1)ШєЁЯBPCЃНЁЯDPCЃН60ЁуЃЌдђЁЯCPDЪЧжБОЖABЕФЁАЛиа§НЧЁБТ№ЃПВЂЫЕУїРэгЩЃЛ
(2)Шє![]() ЕФГЄЮЊ
ЕФГЄЮЊ![]() ІаЃЌЧѓЁАЛиа§НЧЁБЁЯCPDЕФЖШЪ§ЃЛ
ІаЃЌЧѓЁАЛиа§НЧЁБЁЯCPDЕФЖШЪ§ЃЛ
(3)ШєжБОЖABЕФЁАЛиа§НЧЁБЮЊ120ЁуЃЌЧвЁїPCDЕФжмГЄЮЊ24+13![]() ЃЌжБНгаДГіAPЕФГЄЃЎ
ЃЌжБНгаДГіAPЕФГЄЃЎ

ЁОД№АИЁП(1)ЁЯCPDЪЧжБОЖABЕФЁАЛиа§НЧЁБЃЌРэгЩМћНтЮіЃЛ(2)ЁАЛиа§НЧЁБЁЯCPDЕФЖШЪ§ЮЊ45ЁуЃЛ(3)ТњзуЬѕМўЕФAPЕФГЄЮЊ3Лђ23ЃЎ
ЁОНтЮіЁП
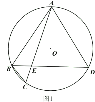
ЃЈ1ЃЉгЩЁЯCPDЁЂЁЯBPCЕУЕНЁЯAPDЃЌЕУЕНЁЯBPCЃНЁЯAPDЃЌЫљвдЁЯCPDЪЧжБОЖABЕФЁАЛиа§НЧЁБЃЛЃЈ2ЃЉРћгУCDЛЁГЄЙЋЪНЧѓГіЁЯCODЃН45ЁуЃЌзїCEЁЭABНЛЁбOгкEЃЌСЌНгPEЃЌРћгУЁЯCPDЮЊжБОЖABЕФЁАЛиа§НЧЁБЃЌЕУЕНЁЯAPDЃНЁЯBPCЃЌЁЯOPEЃНЁЯAPDЃЌЕУЕНЁЯOPE+ЁЯCPD+ЁЯBPCЃН180ЁуЃЌМДЕуDЃЌPЃЌEШ§ЕуЙВЯпЃЌЁЯCEDЃН![]() ЁЯCODЃН22.5ЁуЃЌ
ЁЯCODЃН22.5ЁуЃЌ
ЕУЕНЁЯOPEЃН90ЁуЉ22.5ЁуЃН67.5ЁуЃЌдђЁЯAPDЃНЁЯBPCЃН67.5ЁуЃЌЫљвдЁЯCPDЃН45ЁуЃЛЃЈ3ЃЉЗжГіЧщПіPдкOAЩЯЛђепOBЩЯЕФЧщПіЃЌдкOAЩЯЪБЃЌЭЌРэЃЈ2ЃЉЕФЗНЗЈЕУЕНЕуDЃЌPЃЌFдкЭЌвЛЬѕжБЯпЩЯЃЌЕУЕНЁїPCFЪЧЕШБпШ§НЧаЮЃЌСЌНгOCЃЌODЃЌЙ§ЕуOзїOGЁЭCDгкGЃЌ
РћгУsinЁЯDOGЃЌЧѓЕУCDЃЌРћгУжмГЄЧѓЕУDFЃЌЙ§OзїOHЁЭDFгкHЃЌРћгУЙДЙЩЖЈРэЧѓЕУOPЃЌНјЖјЕУЕНAPЃЛдкOBЩЯЪБЃЌЭЌРэOAМЦЫуЗНЗЈМДПЩ
ЁЯCPDЪЧжБОЖABЕФЁАЛиа§НЧЁБЃЌ
РэгЩЃКЁпЁЯCPDЃНЁЯBPCЃН60ЁуЃЌ
ЁрЁЯAPDЃН180ЁуЉЁЯCPDЉЁЯBPCЃН180ЁуЉ60ЁуЉ60ЁуЃН60ЁуЃЌ
ЁрЁЯBPCЃНЁЯAPDЃЌ
ЁрЁЯCPDЪЧжБОЖABЕФЁАЛиа§НЧЁБЃЛ
(2)ШчЭМ1ЃЌЁпABЃН26ЃЌ
ЁрOCЃНODЃНOAЃН13ЃЌ
ЩшЁЯCODЃНnЁуЃЌ
Ёп![]() ЕФГЄЮЊ
ЕФГЄЮЊ![]() ІаЃЌ
ІаЃЌ
Ёр![]()
ЁрnЃН45ЃЌ
ЁрЁЯCODЃН45ЁуЃЌ
зїCEЁЭABНЛЁбOгкEЃЌСЌНгPEЃЌ
ЁрЁЯBPCЃНЁЯOPEЃЌ
ЁпЁЯCPDЮЊжБОЖABЕФЁАЛиа§НЧЁБЃЌ
ЁрЁЯAPDЃНЁЯBPCЃЌ
ЁрЁЯOPEЃНЁЯAPDЃЌ
ЁпЁЯAPD+ЁЯCPD+ЁЯBPCЃН180ЁуЃЌ
ЁрЁЯOPE+ЁЯCPD+ЁЯBPCЃН180ЁуЃЌ
ЁрЕуDЃЌPЃЌEШ§ЕуЙВЯпЃЌ
ЁрЁЯCEDЃН![]() ЁЯCODЃН22.5ЁуЃЌ
ЁЯCODЃН22.5ЁуЃЌ
ЁрЁЯOPEЃН90ЁуЉ22.5ЁуЃН67.5ЁуЃЌ
ЁрЁЯAPDЃНЁЯBPCЃН67.5ЁуЃЌ
ЁрЁЯCPDЃН45ЁуЃЌ
МДЃКЁАЛиа§НЧЁБЁЯCPDЕФЖШЪ§ЮЊ45ЁуЃЌ
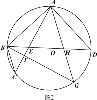
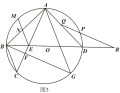
(3)ЂйЕБЕуPдкАыОЖOAЩЯЪБЃЌШчЭМ2ЃЌЙ§ЕуCзїCFЁЭABНЛЁбOгкFЃЌСЌНгPFЃЌ
ЁрPFЃНPCЃЌ
ЭЌ(2)ЕФЗНЗЈЕУЃЌЕуDЃЌPЃЌFдкЭЌвЛЬѕжБЯпЩЯЃЌ
ЁпжБОЖABЕФЁАЛиа§НЧЁБЮЊ120ЁуЃЌ
ЁрЁЯAPDЃНЁЯBPCЃН30ЁуЃЌ
ЁрЁЯCPFЃН60ЁуЃЌ
ЁрЁїPCFЪЧЕШБпШ§НЧаЮЃЌ
ЁрЁЯCFDЃН60ЁуЃЌ
СЌНгOCЃЌODЃЌ
ЁрЁЯCODЃН120ЁуЃЌ
Й§ЕуOзїOGЁЭCDгкGЃЌ
ЁрCDЃН2DGЃЌЁЯDOGЃН![]() ЁЯCODЃН60ЁуЃЌ
ЁЯCODЃН60ЁуЃЌ
ЁрDGЃНODsinЁЯDOGЃН13ЁСsin60ЁуЃН![]()
ЁрCDЃН![]() ЃЌ
ЃЌ
ЁпЁїPCDЕФжмГЄЮЊ24+13![]() ЃЌ
ЃЌ
ЁрPD+PCЃН24ЃЌ
ЁпPCЃНPFЃЌ
ЁрPD+PFЃНDFЃН24ЃЌ
Й§OзїOHЁЭDFгкHЃЌ
ЁрDHЃН![]() DFЃН12ЃЌ
DFЃН12ЃЌ
дкRtЁїOHDжаЃЌOHЃН![]()
дкRtЁїOHPжаЃЌЁЯOPHЃН30ЁуЃЌ
ЁрOPЃН10ЃЌ
ЁрAPЃНOAЉOPЃН3ЃЛ
ЂкЕБЕуPдкАыОЖOBЩЯЪБЃЌ
ЭЌЂйЕФЗНЗЈЕУЃЌBPЃН3ЃЌ
ЁрAPЃНABЉBPЃН23ЃЌ
МДЃКТњзуЬѕМўЕФAPЕФГЄЮЊ3Лђ23ЃЎ

ЁОЬтФПЁПдкЫЎЙћЯњЪлЭњМОЃЌФГЫЎЙћЕъЙКНјвЛгХжЪЫЎЙћЃЌНјМлЮЊ20дЊ/ЧЇПЫЃЌЪлМлВЛЕЭгк20дЊ/ЧЇПЫЃЌЧвВЛГЌЙ§32дЊ/ЧЇПЫЃЌИљОнЯњЪлЧщПіЃЌЗЂЯжИУЫЎЙћвЛЬьЕФЯњЪлСПyЃЈЧЇПЫЃЉгыИУЬьЕФЪлМлxЃЈдЊ/ЧЇПЫЃЉТњзуШчЯТБэЫљЪОЕФвЛДЮКЏЪ§ЙиЯЕЃЎ
ЯњЪлСПyЃЈЧЇПЫЃЉ | Ё | 34.8 | 32 | 29.6 | 28 | Ё |
ЪлМлxЃЈдЊ/ЧЇПЫЃЉ | Ё | 22.6 | 24 | 25.2 | 26 | Ё |
ЃЈ1ЃЉФГЬьетжжЫЎЙћЕФЪлМлЮЊ23.5дЊ/ЧЇПЫЃЌЧѓЕБЬьИУЫЎЙћЕФЯњЪлСПЃЎ
ЃЈ2ЃЉШчЙћФГЬьЯњЪлетжжЫЎЙћЛёРћ150дЊЃЌФЧУДИУЬьЫЎЙћЕФЪлМлЮЊЖрЩйдЊЃП