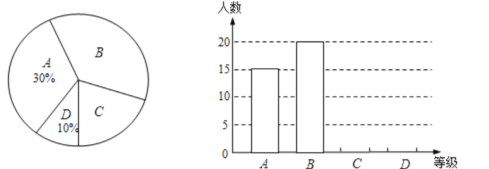
��Ŀ����
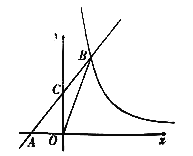
����Ŀ����ͼ1������ABCD��һ��BC��ֱ������ϵ��x���ϣ��۵���AD��ʹ��D����x���ϵ�F�����ۺ�ΪAE����֪AB��8��AD��10�������B����Ϊ��m��0��������m��0��
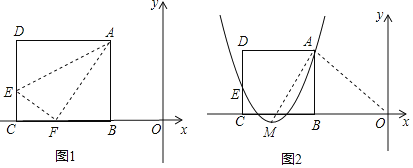
��1�����E��F�����꣨�ú�m��ʽ�ӱ�ʾ����
��2������OA������OAF�ǵ��������Σ���m��ֵ��
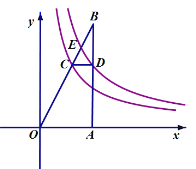
��3����ͼ2����������y��a��x��m+6��2+h����A��E���㣬�䶥��ΪM������AM������OAM��90������a��h��m��ֵ��
���𰸡���1����E������Ϊ��m��10��3������F������Ϊ��m��6��0������2��m����6��4��![]() ����3��a��
����3��a��![]() ��h����1��m����12
��h����1��m����12
��������
��1�������ı���ABCD�Ǿ����Լ����۵��Գ��Եó�AF=AD=10��EF=DE���������BF�ij������ɵó�E��F������ꣻ
��2��������������ۣ���AO=AF��OF=FA��AO=OF�����õ������������ʺ��ɶ���������ɣ�
��3����E��m+10��3����A��m��8����������κ�������ʽ�ó�M������꣬��֤��AOB�ס�AMG�������������������ʿ����m��ֵ���ɣ�
�⣺��1�����ı���ABCD�Ǿ��Σ�AB��8��AD��10��
��AD��BC��10��AB��CD��8����D����DCB����ABC��90����
���۵��Գ��ԣ�AF��AD��10��FE��DE��
��Rt��ABF��BF��![]() ��6��
��6��
��FC��4��
��DE��x����CE��8��x��
��Rt��ECF��42+��8��x��2��x2����x��5��
��CE��8��x��3��
�ߵ�B������Ϊ��m��0����
���E��������m��10��3������F��������m��6��0����
��2���������������ۣ�
��AO��AF��
��AB��OF��BF��6��
��OB��BF��6��
��m����6��
��OF��AF����m��6����10����m����4��
��AO��OF��
��Rt��AOB��AO2��OB2+AB2��m2+64��
�ࣨm��6��2��m2+64����m����![]() ��
��
���Ͽɵã�m����6��4��![]() ��
��
��3���ɣ�1��֪A��m��8����E��m��10��3����
��������y��a��x��m+6��2+h����A��E���㣬
��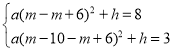 ��
��
��ã�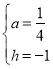 ��
��
��������ߵĽ���ʽΪy��![]() ��x��m+6��2��1��
��x��m+6��2��1��
���M��������m��6����1����
��Գ��ύAD��G��
��G��m��6��8����
��AG��6��GM��8������1����9��
�ߡ�OAB+��BAM��90������BAM+��MAG��90����
���OAB����MAG��
�֡ߡ�ABO����MGA��90����
���AOB�ס�AMG��
��![]() ��
��
��![]() ��
��
��ã�m����12��
���Ͽɵã�a��![]() ��h����1��m����12��
��h����1��m����12��