题目内容
【题目】若关于x的不等式组
无解，且关于y的分式方程
有非正整数解，则符合条件的所有整数k的值之和为（ ）
A.﹣7B.﹣12C.﹣20D.﹣34
【答案】B
【解析】
先根据不等式组无解解出k的取值范围，再解分式方程得y＝
，根据方程有解和非正整数解进行综合考虑k的取值，最后把这几个数相加即可．
∵不等式组
无解，
∴10+2k＞2+k，解得k＞﹣8．
解分式方程
，两边同时乘（y+3），得
ky﹣6＝2（y+3）﹣4y，
解得y＝．
因为分式方程有解，∴≠﹣3，即k+2≠﹣4，解得k≠﹣6．
又∵分式方程的解是非正整数解，∴k+2＝﹣1，﹣2，﹣3，﹣6，﹣12．
解得k＝﹣3，﹣4，﹣5，﹣8，﹣14．
又∵k＞﹣8，
∴k＝﹣3，﹣4，﹣5．
则﹣3﹣4﹣5＝﹣12．
故选：B．
练习册系列答案
相关题目
【题目】在6.26国际禁毒日到来之际，重庆市教委为了普及禁毒知识，提高禁毒意识，举办了“关爱生命，拒绝毒品”的知识竞赛．某校初一、初二年级分别有300人，现从中各随机抽取20名同学的测试成绩进行调查分析，成绩如下：
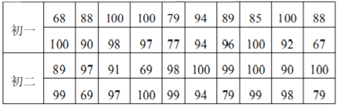
（1）根据上述数据，将下列表格补充完成．
（整理、描述数据）：
分数段 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 |
初一人数 | 2 | _______ | _______ | 12 |
初二人数 | 2 | 2 | 1 | 15 |
（分析数据）：样本数据的平均数、中位数、满分率如表：
年级 | 平均数 | 中位数 | 满分率 |
初一 |
| 93 | ________ |
初二 |
| ________ |
|
（得出结论）：
（2）估计该校初一、初二年级学生在本次测试成绩中可以得到满分的人数共______人；
（3）你认为哪个年级掌握禁毒知识的总体水平较好，请从两个方面说明你的理由．
