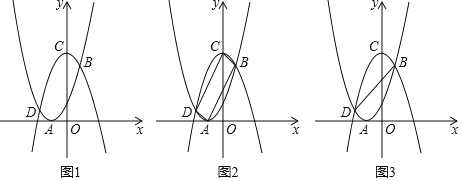
题目内容
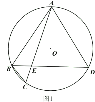
【题目】已知![]() 内接于圆
内接于圆![]() ,点
,点![]() 为弧
为弧![]() 上一点,连接
上一点,连接![]() 交
交![]() 于点
于点![]() ,
,![]() .
.
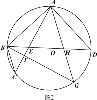
(1)如图1,求证:弧![]() 弧
弧![]() ;
;
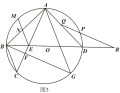
(2)如图2,过![]() 作
作![]() 于点
于点![]() ,交圆
,交圆![]() 点
点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,且
,且![]() ,求
,求![]() 的度数;
的度数;
(3)如图3,在(2)的条件下,圆![]() 上一点
上一点![]() 与点
与点![]() 关于
关于![]() 对称,连接
对称,连接![]() ,交
,交![]() 于点
于点![]() ,点
,点![]() 为弧
为弧![]() 上一点,
上一点,![]() 交
交![]() 于点
于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,
,![]() ,
,![]() 的周长为20,
的周长为20,![]() ,求圆
,求圆![]() 半径.
半径.
【答案】(1)见解析;(2)∠CAG=45°;(3)r=![]()
【解析】
(1)证∠ABD=∠ACB可得;
(2)如下图,△AHD绕点A旋转至△ALE处,使得点D与点B重合,证△ALE≌△AHE,利用勾股定理逆定理推导角度;
(3)如下图,延长QR交AB于点T,分别过点N、Q作BD的垂线,交于点V,I,取QU=AE,过点U作UK垂直BD.先证△AEN≌△QUD,再证△NVE≌△RKU,可得到NV=KR=DK,进而求得OB的长.
(1)∵∠CED是△BEC的外角,∴∠CED=∠EBC+∠BCA
∵∠ABC=∠ABD+∠EBC
又∵∠CED=∠ABC
∴∠ABD=∠ACB
∴弧AB=弧AD
(2)如下图,△AHD绕点A旋转至△ALE处,使得点D与点B重合
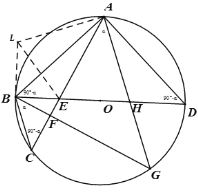
∵△ALB是△AHD旋转所得
∴∠ABL=∠ADB,AL=AH
设∠CAG=a,则∠CBG=a
∵BG⊥AC
∴∠BCA=90°-a,∴∠ADB=∠ABD=90°-a
∴在△BAD中,BAE+∠HAD=180-a-(90°-a)-(90°-a)=a
∴∠LAE=∠EAH=a
∵LA=AH,AE=AE
∴△ALE≌△AHE,∴LE=EH
∵HD=LB,![]()
∴△LBE为直角三角形
∴∠LBE=(90°-a)+(90°-a)=90°,解得:a=45°
∴∠CAG=45°
(3)如下图,延长QR交AB于点T,分别过点N、Q作BD的垂线,交于点V,I,取QU=AE,过点U作UK垂直BD
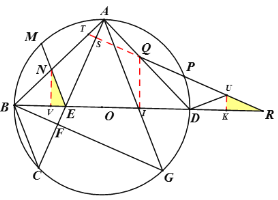
由(2)得∠BAD=90°
∴点O在BD上
设∠R=n,则∠SER=∠BEC=∠MEB=90°-n
∴∠AEN=2n
∵SQ⊥AC
∴∠TAS=∠AQS=∠DQR,AN=QD
∵QU=AE
∴△AEN≌△QUD
∴∠QUD=∠AEN=2n
∴UD=UR=NE,
∵△ANE的周长为20
∴QD+QR=20
在△DQR中,QD=7
∵∠ENR=∠UDK=∠R=n
∴△NVE≌△RKU
∴NV=KR=DK=![]()
∴BN=5
∴BD=12![]() ,OB=6
,OB=6![]()

 阅读快车系列答案
阅读快车系列答案