题目内容
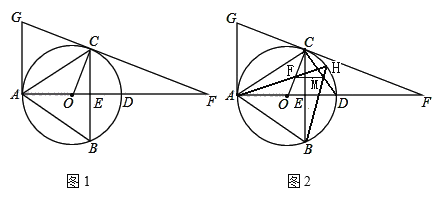
【题目】如图1,△ABC内接于⊙O,直径AD交BC于点E,延长AD至点F,使DF=2OD,连接FC并延长交过点A的切线于点G,且满足AG∥BC,连接OC,若cos∠BAC=![]() ,BC=8.
,BC=8.
(1)求证:CF是⊙O的切线;
(2)求⊙O的半径OC;
(3)如图2,⊙O的弦AH经过半径OC的中点F,连结BH交弦CD于点M,连结FM,试求出FM的长和△AOF的面积.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]() ,
,![]()
【解析】
(1)由DF=2OD,得到OF=3OD=3OC,求得![]() ,推出△COE∽△FOE,根据相似三角形的性质得到∠OCF=∠DEC=90°,于是得到CF是⊙O的切线;
,推出△COE∽△FOE,根据相似三角形的性质得到∠OCF=∠DEC=90°,于是得到CF是⊙O的切线;
(2)利用三角函数值,设OE=x,OC=3x,得到CE=3,根据勾股定理即可得到答案;
(3)连接BD,根据圆周角定理得到角相等,然后证明△AOF∽△BDM,由相似三角形的性质,得到FM为中位线,即可求出FM的长度,由相似三角形的性质,以及中线分三角形的面积为两半,即可求出面积.
解:(1) ∵DF=2OD,
∴OF=3OD=3OC,
∴![]() ,
,
∵∠COE=∠FOC,
∴△COE∽△FOE,
∴∠OCF=∠DEC=90°,
∴CF是⊙O的切线;
(2)∵∠COD=∠BAC,
∴cos∠BAC=cos∠COE=![]() ,
,
∴设OE=x,OC=3x,
∵BC=8,
∴CE=4,
∵CE⊥AD,
∴OE2+CE2=OC2,
∴x2+42=9x2,
∴x=![]() (负值已舍去),
(负值已舍去),
∴OC=3x=![]() ,
,
∴⊙O的半径OC为![]() ;
;
(3)如图,连结BD,
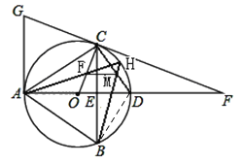
由圆周角定理,则∠OAF=∠DBM,![]() ,
,
∵BC⊥AD,
∴![]() ,
,
∴∠ADC=∠ADB,
∴![]() ,
,
∴△AOF∽△BDM;
∵点F是OC的中点,
∴AO:OF=BD:DM=2,
又∵BD=DC,
∴DM=CM,
∴FM为中位线,
∴FM=![]()
∴S△AOF: S△BDM=(![]() :
:![]() )2
)2 ![]() ;
;
∵![]() ;
;
∴S△AOF=![]() =
=![]() ;
;

 口算能手系列答案
口算能手系列答案【题目】在6.26国际禁毒日到来之际,重庆市教委为了普及禁毒知识,提高禁毒意识,举办了“关爱生命,拒绝毒品”的知识竞赛.某校初一、初二年级分别有300人,现从中各随机抽取20名同学的测试成绩进行调查分析,成绩如下:
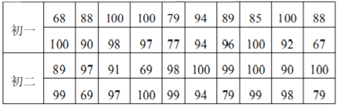
(1)根据上述数据,将下列表格补充完成.
(整理、描述数据):
分数段 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 |
初一人数 | 2 | _______ | _______ | 12 |
初二人数 | 2 | 2 | 1 | 15 |
(分析数据):样本数据的平均数、中位数、满分率如表:
年级 | 平均数 | 中位数 | 满分率 |
初一 |
| 93 | ________ |
初二 |
| ________ |
|
(得出结论):
(2)估计该校初一、初二年级学生在本次测试成绩中可以得到满分的人数共______人;
(3)你认为哪个年级掌握禁毒知识的总体水平较好,请从两个方面说明你的理由.