题目内容
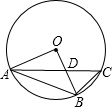
如图，PA、PB切⊙O于A、B两点，C在
AB上，过C点的切线交PA于E，交PB于F，若∠APB=50°．则∠EOF=（ ）
 |
| AB |
| A．45° | B．50° | C．65° | D．75° |
连接OC，
∵PA、PB切⊙O于A、B两点，过C点的切线交PA于E，交PB于F，
∴OA⊥PA，OB⊥PB，∠AOE=∠COE=
∠AOC，∠BOF=∠COF=
∠BOC，
∴∠PAO=∠PBO=90°，
∵∠APB=50°，
∴∠AOB=360°-90°-90°-50°=130°，
∴∠EOF=∠COE+∠COF=
∠AOC+
∠BOC=
（∠AOC+∠BOC）
∠AOB=65°．
故选C．
∵PA、PB切⊙O于A、B两点，过C点的切线交PA于E，交PB于F，
∴OA⊥PA，OB⊥PB，∠AOE=∠COE=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠PAO=∠PBO=90°，
∵∠APB=50°，
∴∠AOB=360°-90°-90°-50°=130°，
∴∠EOF=∠COE+∠COF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故选C．
练习册系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
关于x的函数解析式（要指出函数的定义域）
过点D作DF⊥OE交EC于点F．
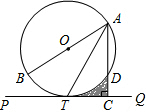
于E，且BE=BD时，求∠A的度数．
