题目内容
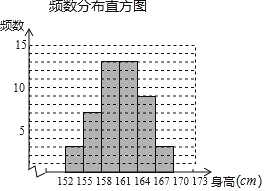
【题目】下表统计的是甲、乙两班男生的身高情况,根据统计表绘制了如下不完整的统计图.
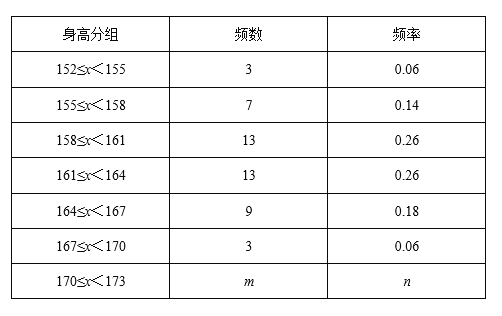
根据以上统计表完成下列问题:
(1)统计表中的m= ,n= ,并将频数分布直方图补充完整;
(2)在这次测量中两班男生身高的中位数在 范围内;
(3)在身高不低于167cm的男生中,甲班有2人.现从这些身高不低于167cm的男生中随机推选2人补充到学校国旗护卫队中,请用列表或画树状图的方法求出这两人都来自相同班级的概率.
【答案】(1)2,0.04,图见解析;(2)161≤x≤164;(3)两人都来自相同班级的概率为![]() .
.
【解析】
(1)先求出总人数,由总人数减去已知频数得出m的值,由频率公式求出n的值即可;
(2)根据中位数的定义即可判断;
(3)画出树状图即可解决问题.
解:(1)∵3÷0.06=50(人),
∴m=50﹣3﹣7﹣13﹣13﹣9﹣3=2,n=2÷50=0.04;
故答案为:2,0.04,
补图:
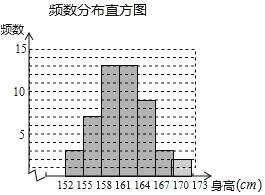
(2)观察表格可知中位数在 161≤x<164内,
故答案为:161≤x≤164;
(3)身高不低于167cm的男生共有5人,
画树状图:

共有20个等可能的结果,两人都来自相同班级的结果有8个,
∴两人都来自相同班级的概率为![]() =
=![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】今年5月份,十八中九年级学生参加了中考体育模拟考试,为了了解该校九年级(1)班同学的中考体育情况,对全班学生的中考体育成绩进行了统计,并绘制以下不完整的频数分布表和扇形统计图,根据图表中的信息解答下列问题:
分组 | 分数段(分)) | 频数 |
A | 26≤x<31 | 2 |
B | 31≤x<36 | 5 |
C | 36≤x<41 | 15 |
D | 41≤x<46 | m |
E | 46≤x<51 | 10 |
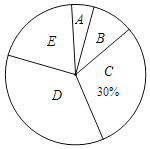
(1)求全班学生人数和m的值.
(2)求扇形统计图中的E对应的扇形圆心角的度数;
(3)该班中考体育成绩满分共有3人,其中男生2人,女生1人,现需从这3人中随机选取2人到八年级进行经验交流,请用“列表法”或“画树状图法”求出恰好选到一男一女的概率.