Question

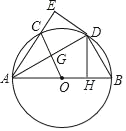
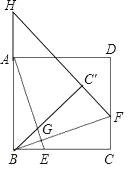
【题目】如图，已知在Rt△ABC中，∠ABC＝90°，点O是AB边上一点，以O为圆心OB为半径的⊙O与边AB相交于点E，与AC边相切于D点，连接OC交⊙O于点F．

（1）连接DE，求证：OC∥DE；

（2）若⊙O的半径为3．

①连接DF，若四边形OEDF为菱形，弧BD的长为_____（结果保留π）

②若AE＝2，则AD的长为_____．

Answer 1

【答案】（1）见解析；（2）①2π；②4.

【解析】

（1）利用HL可证明Rt△OCD≌Rt△OCB，可得∠COD＝∠COB，利用三角形外角性质可得∠DOB＝∠ODE+∠OED，即可证明∠DOC＝∠ODE，即可得OC//DE；（2）①根据菱形的性质可求出∠BOD，利用弧长公式即可得答案；②由DE∥OC，推出＝＝，设AD＝2k，CD＝3k，由Rt△OCD≌Rt△OCB，可得BC＝CD＝3k，在Rt△ABC中，利用勾股定理构建方程即可解决问题．

（1）证明：连接OD．

∵AC是切线，

∴OD⊥AC，∠ODC＝∠OBC＝90°，

∵OC＝OC，OD＝OB，

∴Rt△OCD≌Rt△OCB（HL），

∴∠COD＝∠COB，

∵OD＝OE，

∴∠ODE＝∠OED，

∵∠DOB＝∠ODE+∠OED，

∴∠DOC＝∠ODE，

∴DE∥OC．

（2）①∵四边形DEOF是菱形，

∴DF＝OD＝OF，

∴△ODF是等边三角形，

∴∠DOF＝60°，

∴∠BOD＝2∠DOC＝120°，

∴的长＝＝2π．

故答案为2π．

②∵DE∥OC，

∴＝＝，

设AD＝2k，CD＝3k，

∵Rt△OCD≌Rt△OCB，

∴BC＝CD＝3k，

在Rt△ABC中，则有25k2＝9k2+82，

∴k＝2或﹣2（舍弃），

∴AD＝4．

故答案为4．