题目内容
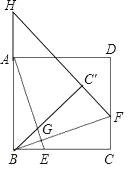
【题目】如图,已知在矩形ABCD中,AD=8,CD=4,点E从点D出发,沿线段DA以每秒1个单位长的速度向点A方向移动,同时点F从点C出发,沿射线CD方向以每秒2个单位长的速度移动,当B,E,F三点共线时,两点同时停止运动.设点E移动的时间为t(秒).
(1)求当t为何值时,两点同时停止运动;
(2)设四边形BCFE的面积为S,求S与t之间的函数关系式,并写出t的取值范围;
(3)求当t为何值时,以E,F,C三点为顶点的三角形是等腰三角形;
(4)求当t为何值时,∠BEC=∠BFC.

【答案】(1)当t=4时,两点同时停止运动;(2)![]() .(
.(![]() );
);
(3)当t的值为4,![]() ,
,![]() 时,以E,F,C三点为顶点的三角形是等腰三角形;
时,以E,F,C三点为顶点的三角形是等腰三角形;
(4)当t=![]() 时,∠BEC=∠BFC.
时,∠BEC=∠BFC.
【解析】
(1)由题意分析可得当B,E,F三点共线时,两点同时停止运动,此时可得到:△FED∽△FBC,同时对应的边都可以用t表示,得到![]() ,求出t即可;
,求出t即可;
(2)四边形BCFE的面积=三角形BCE的面积+三角形EFC的面积;通过题意得ED=t,CF=2t,即可表示出S与t的函数关系;
(3)以E,F,C三点为顶点的三角形是等腰三角形,则需要分类讨论三角形谁为底,谁为高:①若EF=EC时,则点F只能在CD的延长线上;②若EC=FC时;③若EF=FC时;再分别用含t的式子表示出对应边的平方,解得即可。(注意取舍)
(4)由题意得:在Rt△BCF和Rt△CDE中,∵∠BCF=∠CDE=90°,![]() Rt△BCF∽Rt△CDE.∠BCE=∠CED.若∠BEC=∠BFC,则∠BEC=∠BCE.即BE=BC=8.
Rt△BCF∽Rt△CDE.∠BCE=∠CED.若∠BEC=∠BFC,则∠BEC=∠BCE.即BE=BC=8.![]() ,即
,即![]() ,即可求出t的值。(注意取舍)
,即可求出t的值。(注意取舍)
解:(1)当B,E,F三点共线时,两点同时停止运动,如图所示。
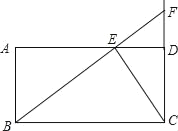
由题意可知:ED=t,BC=8,FD=2t﹣4,FC=2t.
∵ED∥BC,
∴△FED∽△FBC.
∴![]() .
.
∴![]() .
.
解得t=4.
∴当t=4时,两点同时停止运动;
(2)∵ED=t,CF=2t,
∴![]() .
.
即![]() .(
.(![]() );
);
(3)①若EF=EC时,则点F只能在CD的延长线上,
∵![]() ,
,
![]() ,
,
∴![]() .
.
∴t=4或t=0(舍去);
②若EC=FC时,
∵![]() ,
,![]() ,
,
∴![]()
∴![]() ;
;
③若EF=FC时,
∵![]() ,
,![]() ,
,
∴![]() .
.
∴t1=![]() (舍去),t2=
(舍去),t2=![]() .
.
∴当t的值为4,![]() ,
,![]() 时,以E,F,C三点为顶点的三角形是等腰三角形;
时,以E,F,C三点为顶点的三角形是等腰三角形;
(4)在Rt△BCF和Rt△CDE中,
∵∠BCF=∠CDE=90°,![]() ,
,
∴Rt△BCF∽Rt△CDE.
∴∠BFC=∠CED.
∵AD∥BC,
∴∠BCE=∠CED.
若∠BEC=∠BFC,则∠BEC=∠BCE.
∴BE=BC.
∵![]() ,
,
∴![]() .
.
∴t1=![]() (舍去),t2=
(舍去),t2=![]() .
.
∴当t=![]() 时,∠BEC=∠BFC.
时,∠BEC=∠BFC.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案【题目】某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于80元,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/千克) | 50 | 60 | 70 |
销售量y(千克) | 100 | 80 | 60 |
(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为W(元),则当售价x定为多少元时,厂商每天能获得最大利润?最大利润是多少?
(3)如果超市要获得每天不低于1350元的利润,且符合超市自己的规定,那么该商品每千克售价的取值范围是多少?请说明理由.