Question

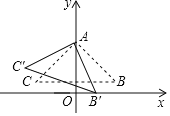
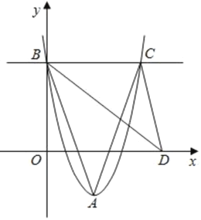
【题目】如图，在平面直角坐标系中，点A是抛物线y＝ax2+bx+c的顶点，点B（0，2）是抛物线与y轴的交点，直线BC平行于x轴，交抛物线于点C，D为x轴上任意一点，若S△ABC＝3，S△BCD＝2，则点A的坐标为_____．

Answer 1

【答案】（1，﹣1）

【解析】

根据△BCD的面积求得BC，即可求得对称轴，根据△ABC的面积即可求得A的纵坐标，从而求得A的坐标．

∵点B（0，2）是抛物线与y轴的交点，直线BC平行于x轴，交抛物线于点C，

∴B、C关于对称轴对称，

∵S△BCD＝BCOB＝2，B（2，0），

∴BC＝2，

∴C（2，2），

∴对称轴为直线x＝＝1，

∵S△ABC＝BC（2﹣yA）＝3，

∴y＝﹣1，

∴A（1，﹣1），

故答案为：（1，﹣1）．