题目内容
【题目】已知:抛物线![]() ,经过点A(-1,-2),B(0,1).
,经过点A(-1,-2),B(0,1).
(1)求抛物线的关系式及顶点P的坐标.
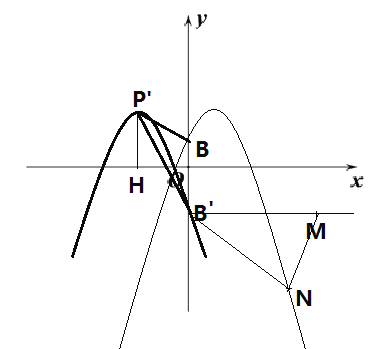
(2)若点B′与点B关于x轴对称,把(1)中的抛物线向左平移m个单位,平移后的抛物线经过点B′,设此时抛物线顶点为点P′.
①求∠P′B B′的大小.
②把线段P′B′以点B′为旋转中心顺时针旋转120°,点P′落在点M处,设点N在(1)中的抛物线上,当△MN B′的面积等于6![]() 时,求点N的坐标.
时,求点N的坐标.
【答案】(1)![]() ,顶点坐标
,顶点坐标![]() ;(2)①
;(2)①![]() ,②当
,②当![]() 时,点
时,点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
【解析】
(1)把点A(-1,-2)B(0,1)代入![]() 即可求出解析式;(2)①设抛物线平移后为
即可求出解析式;(2)①设抛物线平移后为![]() ,代入点B’(0,-1)即可求出m,得出顶点坐标
,代入点B’(0,-1)即可求出m,得出顶点坐标
![]() ,连结
,连结![]() ,P’B’,作P’H⊥y轴,垂足为
,P’B’,作P’H⊥y轴,垂足为![]() ,得
,得![]() ,HB=1,P’B=2
,HB=1,P’B=2
求出![]() , 得
, 得![]() ,故可得
,故可得![]() 的度数
的度数
②根据题意作出图形,根据旋转的性质与![]() ,解得三角形的高
,解得三角形的高![]() ;故设
;故设![]() 或
或![]() 分别代入
分别代入![]() 即可求出N的坐标.
即可求出N的坐标.
(1)把点A(-1,-2)B(0,1)代入![]() 得
得![]() 解得
解得![]()
∴抛物线的关系式为:![]()
得y=-(x-1)2;
∴顶点坐标为![]() .
.
(2)①设抛物线平移后为![]() ,代入点B’(0,-1)得,-1=-(m-1)2+2解得
,代入点B’(0,-1)得,-1=-(m-1)2+2解得![]() ,
,![]() (舍去);
(舍去);
∴![]() ,得顶点
,得顶点![]()
连结![]() ,P’B’,作P’H⊥y轴,垂足为
,P’B’,作P’H⊥y轴,垂足为![]() ,得
,得![]() ,HB=1,P’B=
,HB=1,P’B=![]() =2
=2
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
②∵![]() ,
,![]() 即
即![]() ,
,
∴![]() ;
;
∵线段![]() 以点
以点![]() 为旋转中心顺时针旋转
为旋转中心顺时针旋转![]() ,点
,点![]() 落在点
落在点![]() 处;
处;
∴![]() ,
,![]()
∴![]() 轴,
轴,![]() ;
;
设![]() 在
在![]() 边上的高为
边上的高为![]() ,得:
,得:![]() ,解得
,解得![]() ;
;
∴设![]() 或
或![]() 分别代入
分别代入![]() 得
得![]() 解得:
解得:![]() 或
或![]() ∴
∴![]() 或
或![]() ,
,![]() 方程无实数根舍去,
方程无实数根舍去,
∴综上所述:当![]() 时,点
时,点![]() 的坐标为
的坐标为![]() 或
或![]() .
.

练习册系列答案
相关题目