题目内容
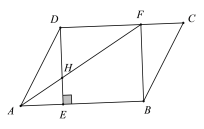
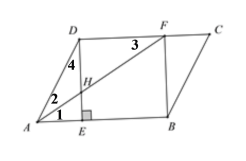
【题目】在平行四边形 ABCD 中,过点 D 作 DE⊥AB 于点 E,点 F 在 CD 上,CF =AE,连接 BF,AF.
(1)求证:四边形 BFDE 是矩形;
(2)若 AF 平分∠BAD,交DE与H点,且 AB=3AE,BF=6,求AH的长.
【答案】(1)证明见解析; (2)4.
【解析】
(1)由CF =AE易得BE=DF.根据有一个角是90度的平行四边形是矩形即可判定.
(2)由AF 平分∠BAD,结合平行四边形性质可知AD=DF,而AB=3AE,即可知AD=DF=2AE,推出∠ADE=30°,由此可以解题.
(1)证明:∵ 在□ABCD中,AB∥CD,AB=CD,
∵CF=AE,
∴AB-AE=CD-CF,
即 BE=DF,
∵BE∥DF,
∴ 四边形DEBF是□DEBF,
∵DE⊥AB,
∴∠DEB=90,
∴四边形 BFDE 是矩形.
(2)解:∵AF 平分∠BAD,
∴∠1=∠2,
∵AB∥CD,
∴∠1=∠3,
∴∠2=∠3,
∴AD=DF,
∵AB=3AE
∴BD=2AE
∵BD=DF,AD=DF
∴AD=2AE,又∠AED=90
∴∠4=30,∠DAE=60
在矩形DEBF中DE=BF=6
∴AE =2![]()
在 RtΔAEH 中,∵∠AEH=90,∠1=![]() ∠DAE=30
∠DAE=30
∴AH=![]() = 4
= 4

 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案【题目】在一个不透明的盒子中装有![]() 个小球,它们除了颜色不同外,其余都相同, 其中有 5 个白球,每次试验前,将盒子中的小球摇匀,随机摸出一个球记下颜色后再放回盒中.下表是摸球试验的一组统计数据:
个小球,它们除了颜色不同外,其余都相同, 其中有 5 个白球,每次试验前,将盒子中的小球摇匀,随机摸出一个球记下颜色后再放回盒中.下表是摸球试验的一组统计数据:
摸球次数( n ) | 50 | 100 | 150 | 200 | 250 | 300 | 500 |
摸到白球次( m ) | 28 | 60 | 78 | 104 | 123 | 152 | 251 |
白球频率( | 0.56 | 0.60 | 0.52 | 0.52 | 0.49 | 0.51 | 0.50 |
由上表可以推算出a大约是( )
A.10B.14C.16D.40
【题目】某校九年级(1)班50名学生需要参加体育“五选一”自选项目测试,班上学生所报自选项目的情况统计如表所示:
自选项目 | 人数 | 频率 |
立定跳远 | b | 0.18 |
三级蛙跳 | 12 | 0.24 |
一分钟跳绳 | 8 | a |
投掷实心球 | 16 | 0.32 |
推铅球 | 5 | 0.10 |
合计 | 50 | 1 |
(1)求a,b的值;
(2)若该校九年级共有400名学生,试估计年级选择“一分钟跳绳”项目的总人数;
(3)在选报“推铅球”的学生中,有3名男生,2名女生,为了了解学生的训练效果,从这5名学生中随机抽取两名学生进行推铅球测试,求所抽取的两名学生中至少有一名女生的概率.