题目内容
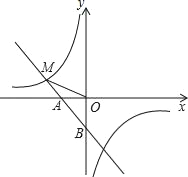
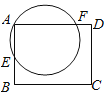
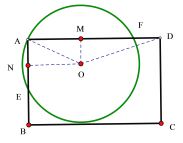
【题目】如图，在矩形ABCD中，过点A的圆O交边AB于点E，交边AD于点F，已知AD=5，AE=2，AF=4．如果以点D为圆心，r为半径的圆D与圆O有两个公共点，那么r的取值范围是______．
【答案】
【解析】
因为以点D为圆心，r为半径的圆D与圆O有两个公共点，则圆D与圆O相交，圆心距满足关系式：|R-r|<d<R+r，求得圆D与圆O的半径代入计算即可.
连接OA、OD，过O点作ON⊥AE，OM⊥AF.
AN=
AE=1，AM=AF=2，MD=AD-AM=3
∵四边形ABCD是矩形
∴∠BAD=∠ANO=∠AMO=90°，
∴四边形OMAN是矩形
∴OM=AN=1
∴OA=
,OD=
∵以点D为圆心，r为半径的圆D与圆O有两个公共点，则圆D与圆O相交
∴
成功训练计划系列答案
倍速训练法直通中考考点系列答案
一卷搞定系列答案
名校作业本系列答案
轻巧夺冠周测月考直通名校系列答案【题目】水果基地为了选出适应市场需求的小西红柿秧苗，在条件基本相同的情况下，把两个品种的小西红柿秧苗各 300 株分别种植在甲、乙两个大棚. 对于市场最为关注的产量和产量的稳定性，进行了抽样调查，从甲、乙两个大棚各收集了 24 株秧苗上的小西红柿的个数，并对数据进行整理、描述和分析。
下面给出了部分信息：（说明：45 个以下为产量不合格，45 个及以上为产量合格，其中 45～65 个为产量良好，65～85 个为产量优秀）
a.补全下面乙组数据的频数分布直方图(数据分成 6 组: 25≤x＜35，35≤x＜45，45≤x＜55，55≤x＜65，65≤x＜75，75≤x＜85):
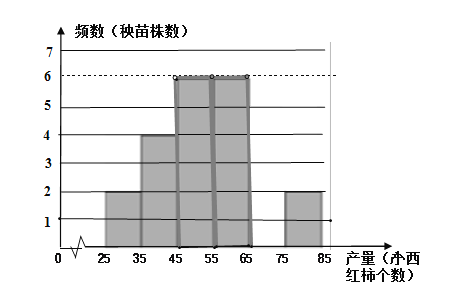
b.乙组数据在产量良好（45≤x＜65）这两组的具体数据为： 46 46 47 47 48 48 55 57 57 57 58 61
c.数据的平均数、众数和方差如下表所示：
大棚 | 平均数 | 中位数 | 众数 | 方差 |
甲 | 52.25 | 51 | 58 | 238 |
乙 | 52.25 | 57 | 210 |
（1）补全乙的频数分布直方图.
（2）写出表中
的值．
（3）根据样本情况，估计乙大棚产量良好及以上的秧苗数为 株．
（4）根据抽样调查情况，可以推断出 大棚的小西红柿秧苗品种更适应市场需求，写出理由．（至少从两个不同的角度说明推断的合理性）．
