��Ŀ����
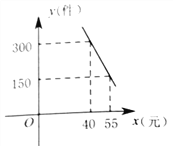
����Ŀ��ij��˾�������²�Ʒ1520kg��ΪѰ����ʵ����ۼ۸�����8��������������470kg��ͳ�Ʒ���ÿ���������y��ǧ�ˣ������ۼ۸�x��Ԫ/ǧ�ˣ�֮�����㺯����ϵy����x+120��
��1��������8���˾���������ֲ�Ʒ�����ۼ۸�Ϊ50Ԫ/ǧ�ˣ�����ÿ�춼������۸����ۣ������µIJ�Ʒ���ö�����ȫ�����ꣿ
��2���ڣ�1���������£���˾��������9�����ʣ��IJ�Ʒ������5����ȫ�����꣬��ʱ��Ҫ����ȷ��һ�����ۼ۸�ʹ���涼���µļ۸����ۣ���ô��ȷ���ļ۸���߲�����ÿǧ�˶���Ԫ���������������
���𰸡���1��ʣ��IJ�Ʒ��Ҫ�����ʱ��Ϊ15�죻��2���¼۸���߲�����ÿǧ��38Ԫ���������������
��������
��1�������ۼ۸�Ϊ50Ԫ/ǧ��ʱ������ÿ���������y��ǧ�ˣ������ۼ۸�x��Ԫ/ǧ�ˣ�֮��Ĺ�ϵʽ���ÿ�����������Ȼ����ÿ��������������ۼ۸ɽ��
ÿ�������y=-50+ 120=70��������⣻
��2������˾��������9������ʣ��IJ�Ʒ����Ϊ410��Ȼ��������ã�5y��410�����ɽ��
�⣺��1�����ۼ۸�Ϊ50Ԫ/ǧ��ʱ��ÿ�����������y����x+120����50+120��70��
��ʣ��IJ�Ʒ��Ҫ�����ʱ��Ϊ��![]() ��15��
��15��
��2����˾��������9���ʣ��IJ�Ʒ����Ϊ��1520��470��9��70��410��
���¼۸�ΪxԪ��������ã�5y��410��
��5����x+120����410��
��ã�x��38��
���¼۸���߲�����ÿǧ��38Ԫ���������������

����Ŀ���������������̳��ﹺ���ܺ���90Ԫ����Ʒ�ס��ҡ��������Σ����мĵ�����20Ԫ���ҵĵ�����40Ԫ������Ʒ��һ�ι���������ǵڶ��ι�������������������Ʒ��һ�ι�������������Ʒ�ڶ��ι����������ȣ����ι�����Ʒ�ס��ҡ������������ܷ������±���
������Ʒ�� ����(��) | ������Ʒ�ҵ� ����(��) | ������Ʒ���� ����(��) | �����ܷ���(Ԫ) | |
��һ�ι��� | 4 | 440 | ||
�ڶ��ι��� | 7 | 490 |
(1)�����ι���ס��ҡ���������Ʒ���������ֱ��Ƕ��٣�
(2)���������̳�������������������������ǰ��������Ʒ�ס��ҡ�������������Ʒ�������ܺ�Ϊa�������й�������Ʒ�����Ǽ���Ʒ������3���������ܷ���Ϊ1 280Ԫ����a����Сֵ��