题目内容
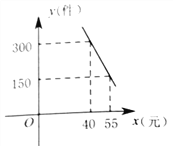
【题目】“扬州漆器”名扬天下,某网店专门销售某种品牌的漆器笔筒,成本为30元/件,每天销售量![]() (件)与销售单价
(件)与销售单价![]() (元)之间存在一次函数关系,如图所示.
(元)之间存在一次函数关系,如图所示.
(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)如果规定每天漆器笔筒的销售量不低于240件,当销售单价为多少元时,每天获取的利润最大,最大利润是多少?
(3)该网店店主热心公益事业,决定从每天的销售利润中捐出150元给希望工程,为了保证捐款后每天剩余利润不低于3600元,试确定该漆器笔筒销售单价的范围.
【答案】(1)![]() ;(2)单价为46元时,利润最大为3840元.(3)单价的范围是45元到55元.
;(2)单价为46元时,利润最大为3840元.(3)单价的范围是45元到55元.
【解析】(1)可用待定系数法来确定y与x之间的函数关系式;
(2)根据利润=销售量×单件的利润,然后将(1)中的函数式代入其中,求出利润和销售单件之间的关系式,然后根据其性质来判断出最大利润;
(3)首先得出w与x的函数关系式,进而利用所获利润等于3600元时,对应x的值,根据增减性,求出x的取值范围.
(1)由题意得:![]()
![]() .
.
故y与x之间的函数关系式为:y=-10x+700,
(2)由题意,得
-10x+700≥240,
解得x≤46,
设利润为w=(x-30)y=(x-30)(-10x+700),
w=-10x2+1000x-21000=-10(x-50)2+4000,
∵-10<0,
∴x<50时,w随x的增大而增大,
∴x=46时,w大=-10(46-50)2+4000=3840,
答:当销售单价为46元时,每天获取的利润最大,最大利润是3840元;
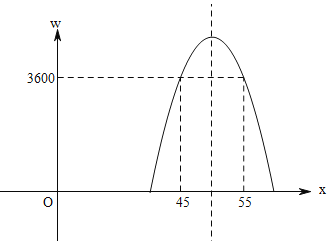
(3)w-150=-10x2+1000x-21000-150=3600,
-10(x-50)2=-250,
x-50=±5,
x1=55,x2=45,
如图所示,由图象得:
当45≤x≤55时,捐款后每天剩余利润不低于3600元.

【题目】已知:二次函数y=ax2+bx+c, y与x的一些对应值如下表:
x | …… | 1 | 0 | 1 | 2 | 3 | 4 | …… |
ax2+bx+c | …… | 3 | 1 | 3 | …… |
(1)根据表格中的数据,确定二次函数解析式为_________________;
(2)填齐表格中空白处的对应值并利用上表,用五点作图法,画出二次函数y=ax2+bx+c的图象.(不必重新列表)
(3)当 1 < x ≤4时,y的取值范围是_________________;