题目内容
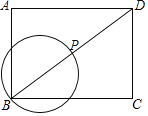
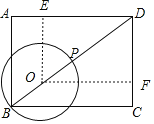
【题目】如图,在矩形ABCD中,AB=3,BC=4,P是对角线BD上的动点,以BP为直径作圆,当圆与矩形ABCD的边相切时,BP的长为__.
【答案】![]() 或
或![]() .
.
【解析】
以O为圆心,BP为直径画圆,作OE⊥AD于E,OF⊥CD于F,设圆O的半径为r,先利用勾股定理求得BD=5;然再分OE=OB和OF=OB两种情况分别求出BP的长即可.
解:BP为直径的圆的圆心为O,作OE⊥AD于E,OF⊥CD于F,如图,
设⊙O的半径为r,
在矩形ABCD中,AB=3,BC=4,
∴BD=![]() =5,
=5,
当OE=OB时,⊙O与AD相切,
∵OE∥AB,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,解得r=
,解得r=![]() ,
,
此时BP=2r=![]() ;
;
当OF=OB时,⊙O与DC相切,
∵OF∥BC,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,解得r=
,解得r=![]() ,
,
此时BP=2r=![]() ;
;
综上所述,BP的长为![]() 或
或![]() .
.
故答案为![]() 或
或![]() .
.

练习册系列答案
相关题目