题目内容
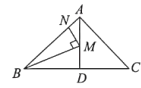
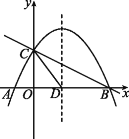
【题目】如图,直角三角形纸片![]() 中,
中,![]() ,
,![]() cm,
cm,![]() cm,点
cm,点![]() 分别在边
分别在边![]() 上,点
上,点![]() 是边
是边![]() 的中点.现将该纸片沿
的中点.现将该纸片沿![]() 折叠,使点
折叠,使点![]() 与点
与点![]() 重合,则
重合,则![]() ______cm.
______cm.
【答案】![]()
【解析】
过点F作FH⊥AB于点H,利用勾股定理可得AB=5,根据点F为BC的中点可得BF=2,根据![]() ,
,![]() 可证△BHF∽△BCA,进而由相似三角形的性质可得
可证△BHF∽△BCA,进而由相似三角形的性质可得![]() ,根据折叠可设AE=FE=x,最后利用Rt△EFH的勾股定理列出方程求解即可.
,根据折叠可设AE=FE=x,最后利用Rt△EFH的勾股定理列出方程求解即可.
解:如图,过点F作FH⊥AB于点H,
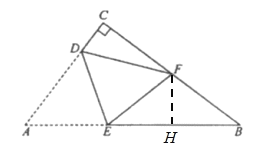
∵![]() ,
,![]() ,
,![]() ,
,
∴![]()
∵点F为BC的中点,BC=4,
∴BF=2,
∵![]() ,FH⊥AB,
,FH⊥AB,
∴![]() ,
,
又∵![]() ,
,
∴△BHF∽△BCA,
∴![]() ,
,
∴![]() ,
,
解得![]() ,
,
∵折叠,
∴设AE=FE=x,
则EH=AB-AE-BH=![]() ,
,
∵在Rt△EFH中,EH2+FH2=EF2,
∴![]()
解得:![]() ,
,
∴![]() ,
,
故答案为:![]() .
.

 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案【题目】如图,己知抛物线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,其对称轴与抛物线相交于点
,其对称轴与抛物线相交于点![]() ,与
,与![]() 轴相交于点
轴相交于点![]() .
.
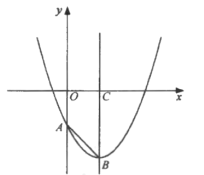
(1)求![]() 的长;
的长;
(2)平移该抛物线得到一条新抛物线,设新抛物线的顶点为![]() .若新抛物线经过原点
.若新抛物线经过原点![]() ,且
,且![]() ,求新抛物线对应的函数表达式.
,求新抛物线对应的函数表达式.
【题目】为培养学生良好学习习惯,某学校计划举行一次“整理错题集”的展示活动,对该校部分学生“整理错题集”的情况进行了一次抽样调查,根据收集的数据绘制了下面不完整的统计图表.
整理情况 | 频数 | 频率 |
非常好 | 0.21 | |
较好 | 70 | 0.35 |
一般 | m | |
不好 | 36 |
请根据图表中提供的信息,解答下列问题:
(1)本次抽样共调查了 名学生;
(2)m= ;
(3)该校有1500名学生,估计该校学生整理错题集情况“非常好”和“较好”的学生一共约多少名?
(4)某学习小组4名学生的错题集中,有2本“非常好”(记为A1、A2),1本“较好”(记为B),1本“一般”(记为C),这些错题集封面无姓名,而且形状、大小、颜色等外表特征完全相同,从中抽取一本,不放回,从余下的3本错题集中再抽取一本,请用“列表法”或“画树形图”的方法求出两次抽到的错题集都是“非常好”的概率.