题目内容
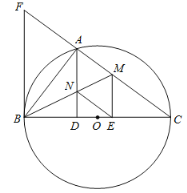
【题目】如图,以BC为直径的⊙O交△CFB的边CF于点A,BM平分∠ABC交AC于点M,AD⊥BC于点D,AD交BM于点N,ME⊥BC于点E,AB2=AF·AC,cos∠ABD=![]() ,AD=12.
,AD=12.
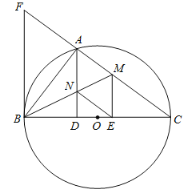
(1)求证:△ABF∽△ACB;
(2)求证:FB是⊙O的切线;
(3)证明四边形AMEN是菱形,并求该菱形的面积S.
【答案】(1)见解析;(2)见解析;(3)见解析,45
【解析】
(1)根据直径所对的圆周角是直角可得∠BAC=90°,从而得出∠BAF=∠BAC=90°,最后根据相似三角形的判定定理即可证出结论;
(2)根据相似三角形的性质可得∠ABF=∠C,然后利用等量代入可得∠FBC=∠ABC+∠ABF=90°,从而证出结论;
(3)根据角平分线的性质可得MA=ME,利用SAS即可证出△AMN≌△EMN,然后根据平行线的性质和等角对等边可证AN=NE=EM=MA,从而证出四边形AMEN是菱形,然后利用锐角三角函数和勾股定理即可求出BD、AD和AB,从而求出DE,然后证出△BND∽△BME,列出比例式即可求出ME,从而求出结论.
(1)证明:![]() BC为⊙O的直径
BC为⊙O的直径
![]() ∠BAC=90°
∠BAC=90°
![]() ∠BAF=∠BAC=90°
∠BAF=∠BAC=90°
又![]() AB2=AF·AC
AB2=AF·AC
![]()
![]()
![]() △ABF∽△ACB
△ABF∽△ACB
(2)证明:
![]() △ABF∽△ACB
△ABF∽△ACB
![]() ∠ABF=∠C
∠ABF=∠C
又![]() ∠ABC+∠C=90°
∠ABC+∠C=90°
![]() ∠FBC=∠ABC+∠ABF=90°
∠FBC=∠ABC+∠ABF=90°
![]() BF是⊙O的切线
BF是⊙O的切线
(3)证明:![]() ME⊥BC,MA⊥AB,BM平分∠ABC
ME⊥BC,MA⊥AB,BM平分∠ABC
![]() MA=ME
MA=ME
![]() ∠AMN=90°-∠ABM=90°-∠EBM=∠EMN
∠AMN=90°-∠ABM=90°-∠EBM=∠EMN
∴AB=BE
∵NM=NM
![]() △AMN≌△EMN
△AMN≌△EMN
![]() AN=NE
AN=NE
又![]() AD⊥BC,ME⊥BC,
AD⊥BC,ME⊥BC,
![]() ME∥AD,
ME∥AD,
![]() ∠ANM=∠EMN,
∠ANM=∠EMN,
![]() ∠ANM=∠AMN
∠ANM=∠AMN
![]() AN=AM
AN=AM
![]() AN=NE=EM=MA,
AN=NE=EM=MA,
![]() 四边形AMEN是菱形.
四边形AMEN是菱形.
![]() cos∠ABD=
cos∠ABD=![]() ,∠ADB=90°
,∠ADB=90°
![]()
![]()
设BD=3x,则AB=5x,AD=![]()
又![]() AD=12,
AD=12,
![]() x=3,
x=3,
![]() BD=9,AB=15,
BD=9,AB=15,
![]() BE=BA=15
BE=BA=15
![]() DE=BE-BD=6
DE=BE-BD=6
![]() ND∥ME,
ND∥ME,
![]() ∠BND=∠BME
∠BND=∠BME
![]() △BND∽△BME
△BND∽△BME
![]()
![]()
设ME=y,则ND=12-y,
![]() ,
,
解得y=![]()
![]() S=
S=![]()

【题目】某学校对全体学生“新冠肺炎”疫情防控知识的掌握情况进行了线上测试,该测试共有![]() 道题,每题
道题,每题![]() 分,满分
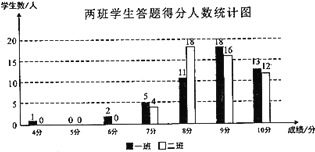
分,满分![]() 分,该校将七年级一班和二班的成绩进行整理,得到如下信息:
分,该校将七年级一班和二班的成绩进行整理,得到如下信息:
班级 | 平均数 | 中位数 | 众数 | 优秀( |
一班 |
|
|
|
|
二班 |
|
|
|
|
请你结合图表中所给信息,解答下列问题:
(1)请直接写出![]() ,
,![]() ,
,![]() 的值;
的值;
(2)你认为哪个班对疫情防控知识掌握较好,请说明理由(选择两个角度说明推断的合理性)
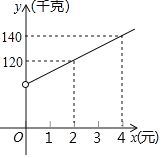
【题目】为培养学生良好学习习惯,某学校计划举行一次“整理错题集”的展示活动,对该校部分学生“整理错题集”的情况进行了一次抽样调查,根据收集的数据绘制了下面不完整的统计图表.
整理情况 | 频数 | 频率 |
非常好 | 0.21 | |
较好 | 70 | 0.35 |
一般 | m | |
不好 | 36 |
请根据图表中提供的信息,解答下列问题:
(1)本次抽样共调查了 名学生;
(2)m= ;
(3)该校有1500名学生,估计该校学生整理错题集情况“非常好”和“较好”的学生一共约多少名?
(4)某学习小组4名学生的错题集中,有2本“非常好”(记为A1、A2),1本“较好”(记为B),1本“一般”(记为C),这些错题集封面无姓名,而且形状、大小、颜色等外表特征完全相同,从中抽取一本,不放回,从余下的3本错题集中再抽取一本,请用“列表法”或“画树形图”的方法求出两次抽到的错题集都是“非常好”的概率.
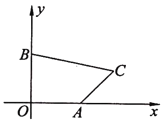
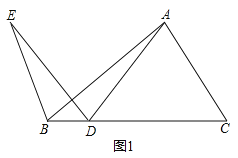
【题目】如图,在![]() 中,点D是线段
中,点D是线段![]() 上的动点,将线段
上的动点,将线段![]() 绕点D逆时针旋转90°得到线段
绕点D逆时针旋转90°得到线段![]() ,连接
,连接![]() .若已知
.若已知![]() ,设B,D两点间的距离为
,设B,D两点间的距离为![]() ,A,D两点间的距离为
,A,D两点间的距离为![]() ,B,E两点间的距离为
,B,E两点间的距离为![]() .
.
小明根据学习函数的经验,分别对函数![]() ,
,![]() 随自变量x的变化而变化的规律进行了探究
随自变量x的变化而变化的规律进行了探究
下面是小明的探究过程,请补全完整:
(1)按照下表中自变量x的值进行取点、画图、测量,分别得到了![]() ,
,![]() 与x的几组对应值,如下表:(说明:补全表格时相关数值保留一位小数)
与x的几组对应值,如下表:(说明:补全表格时相关数值保留一位小数)
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 7.03 | 6.20 | 5.44 | 4.76 | 4.21 | 3.85 | 3.73 | 3.87 | 4.26 |
| a | 5.66 | 4.32 | b | 1.97 | 1.59 | 2.27 | 3.43 | 4.73 |
(2)在同一平面直角坐标系![]() 中,描出补全后的表中各组数值所对应的点
中,描出补全后的表中各组数值所对应的点![]() ,
,![]() ,并画出函数
,并画出函数![]() ,
,![]() 的图象;
的图象;
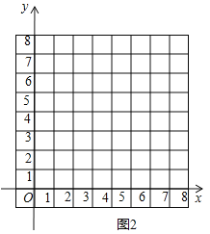
(3)结合函数图象,解决问题:
①当E在线段![]() 上时,
上时,![]() 的长度约为___________cm;
的长度约为___________cm;
②当![]() 为等腰三角形时,
为等腰三角形时,![]() 的长度x约为___________cm.
的长度x约为___________cm.