题目内容
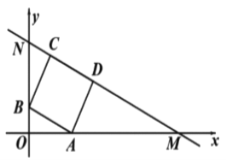
【题目】已知点![]() ,抛物线
,抛物线![]() 与
与![]() 轴从左到右的交点为
轴从左到右的交点为![]() ,
,![]() .
.
(1)若抛物线![]() 经过点
经过点![]() ,求抛物线
,求抛物线![]() 的解析式和顶点坐标;
的解析式和顶点坐标;
(2)当![]() 时,求
时,求![]() 的值;
的值;
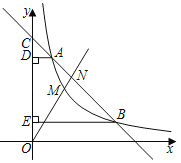
(3)直线![]() 经过点
经过点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,
,
①求点![]() 的坐标;
的坐标;
②若线段![]() 与抛物线
与抛物线![]() 有唯一公共点,直接写出正整数
有唯一公共点,直接写出正整数![]() 的值.
的值.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() 或
或![]() ;(3)①
;(3)①![]() ,②
,②![]() 和
和![]()
【解析】
(1)由抛物线![]() 经过
经过![]() ,把点M代入即可求出
,把点M代入即可求出![]() ,抛物线
,抛物线![]() 的解析式即求出;把抛物线解析式化为顶点式,即可得顶点点坐标;
的解析式即求出;把抛物线解析式化为顶点式,即可得顶点点坐标;
(2)方法一:利用抛物与![]() 轴的交点坐标关于对称轴对称的特点求解,设
轴的交点坐标关于对称轴对称的特点求解,设![]() ,则
,则![]() ,
,![]() ,由抛物线对称轴为直线:
,由抛物线对称轴为直线:![]() ,①当
,①当![]() ,则
,则![]() 可得
可得![]() ,求出
,求出![]() ,此时
,此时![]() 代入抛物线可求出
代入抛物线可求出![]() ;②当
;②当![]() ,则
,则![]() ,此时可出
,此时可出![]() ,此时
,此时![]() 代入抛物线解析式得
代入抛物线解析式得![]() ;综上所述即为
;综上所述即为![]() 的值;
的值;
方法二:利用物线![]() 与
与![]() 轴有两个交点,用判别式得出
轴有两个交点,用判别式得出![]() 的取值范围
的取值范围![]() ,令
,令![]() ,用求根公式表示出方程的解,当
,用求根公式表示出方程的解,当![]() 时,可得两个解的关系
时,可得两个解的关系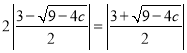 ,解之,即可得
,解之,即可得![]() 的值;
的值;
(3)①把![]() 代入直线
代入直线![]() ,即可得b的值,写出直线解析式,令
,即可得b的值,写出直线解析式,令![]() ,即可求与
,即可求与![]() 轴交于点的纵坐标,即求得
轴交于点的纵坐标,即求得![]() 点坐标;
点坐标;
②由线段![]() 与抛物线
与抛物线![]() 有唯一公共点,联立直线和抛物线的方程,可解得此时符合题意的
有唯一公共点,联立直线和抛物线的方程,可解得此时符合题意的![]() ;当抛物线经过点M时,解得c=2 ,此时抛物线与线段MN有2个公共点,与题意不符;当抛物线往下平移到经过点N时,解得c=-1 ,此时抛物线与线段MN只有交点N,当-1≤c<2时,抛物线与线段MN只有-个公共点,而此时满足条件的正整数c的值为1,综上所述,即可得符合条件的
;当抛物线经过点M时,解得c=2 ,此时抛物线与线段MN有2个公共点,与题意不符;当抛物线往下平移到经过点N时,解得c=-1 ,此时抛物线与线段MN只有交点N,当-1≤c<2时,抛物线与线段MN只有-个公共点,而此时满足条件的正整数c的值为1,综上所述,即可得符合条件的![]() 的值.
的值.
解:(1)![]() 抛物线
抛物线![]() 经过
经过![]() ,
,
![]() ,
,
解得:![]() .
.
![]() ,
,
![]() ,
,
![]() 顶点为
顶点为![]() ,
,
(2)方法一:
设![]() ,则
,则![]() ,
,![]() ,
,
①若![]() ,则
,则![]() ,
,
![]() 抛物线对称轴为直线:
抛物线对称轴为直线:![]() ,点
,点![]() 、
、![]() 关于对称轴对称,
关于对称轴对称,
![]() ,即
,即![]() ,
,
解得:![]() ,
,
![]() 代入抛物线解析式得:
代入抛物线解析式得:![]() ,
,
解得:![]() ;
;
②若![]() ,则
,则![]() ,
,
![]() ,
,
解得:![]() ,
,
![]() 代入抛物线解析式得:
代入抛物线解析式得:![]() ,
,
解得:![]() ;
;
综上所述![]() 的值为
的值为![]() 或
或![]() .
.
方法二:
(2)![]() 抛物线
抛物线![]() 与
与![]() 轴有两个交点,
轴有两个交点,
![]() ,
,
解得![]() ,
,
令![]() ,
,
解得![]() ,
,
![]() 点
点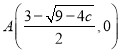 ,
,
点 ,
,
![]() 当
当![]() 时,
时,
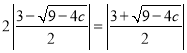 ,
,
![]() 或
或
![]() ,解得
,解得![]() 或
或![]() .
.
(3)①![]() 直线
直线![]() 经过点
经过点![]() ,
,
![]() ,
,
解得:![]() ,
,
![]() 直线解析式为
直线解析式为![]() ,
,
当![]() 时,
时,![]() ,
,
![]() 点
点![]() 坐标为
坐标为![]() .
.
②满足条件的正整数![]() 的值为
的值为![]() 和
和![]() ;
;
理由如下:

当线段![]() 与抛物线
与抛物线![]() 只有一个公共点时,
只有一个公共点时,
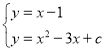 ,
,
∴![]() ,
,
△![]() ,
,
所以![]() ,
,
此时方程的解为 ,
,
∴此时交点在线段![]() 上,满足题意段
上,满足题意段![]() 与抛物线
与抛物线![]() 有唯一公共点;
有唯一公共点;
当抛物线经过点M时,解得c=2 ,此时抛物线与线段MN有2个公共点,与题意不符;
当抛物线往下平移到经过点N时,解得c=-1 ,此时抛物线与线段MN只有交点N,
∴当-1≤c<2时,抛物线与线段MN只有-个公共点
∴此时满足条件的正整数c的值为1;
综上所述,满足条件的正整数c的值为1或3.