题目内容
【题目】如图,一次函数y=kx+b(k≠0)的图象与反比例函数y=![]() (m≠0,x>0)的图象在第一象限内交于点A,B,且该一次函数的图象与y轴正半轴交于点C,过A,B分别作y轴的垂线,垂足分别为D,E.已知A(1,4),
(m≠0,x>0)的图象在第一象限内交于点A,B,且该一次函数的图象与y轴正半轴交于点C,过A,B分别作y轴的垂线,垂足分别为D,E.已知A(1,4),![]() =
=![]() .
.
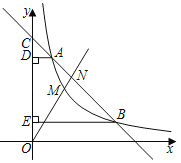
(1)求m的值和一次函数的解析式;
(2)若点M为反比例函数图象在A,B之间的动点,作射线OM交直线AB于点N,当MN长度最大时,直接写出点M的坐标.
【答案】(1)4,y=﹣x+5;(2)(2,2)
【解析】
(1)先把A点坐标代入y=![]() 中求出m得到反比例函数解析式为y=
中求出m得到反比例函数解析式为y=![]() ;再证明△CDA∽△CEB,利用相似比求出BE=4,则利用反比例函数解析式确定B点坐标,然后利用待定系数法求一次函数解析式;
;再证明△CDA∽△CEB,利用相似比求出BE=4,则利用反比例函数解析式确定B点坐标,然后利用待定系数法求一次函数解析式;
(2)利用点A与点B关于直线y=x对称,反比例函数y=﹣![]() 关于y=x对称可判断当OM的解析式为y=x时,MN的长度最大,然后解方程组
关于y=x对称可判断当OM的解析式为y=x时,MN的长度最大,然后解方程组![]() 得此时M点的坐标.
得此时M点的坐标.
(1)把A(1,4)代入y=![]() 得m=1×4=4,
得m=1×4=4,
∴反比例函数解析式为y=![]() ;
;
∵BD⊥y轴,AD⊥y轴,
∴AD∥BE,
∴△CDA∽△CEB,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴BE=4,
当x=4时,y=![]() =
=![]() =1,
=1,
∴B(4,1),
把A(1,4),B(4,1)代入y=kx+b得![]() ,解得
,解得![]() ,
,
∴一次函数解析式为y=﹣x+5;
(2)∵点A与点B关于直线y=x对称,反比例函数y=﹣![]() 关于y=x对称,
关于y=x对称,
∴当OM的解析式为y=x时,MN的长度最大,
解方程组![]() 得
得![]() 或
或![]() ,
,
∴此时M点的坐标为(2,2).

 阅读快车系列答案
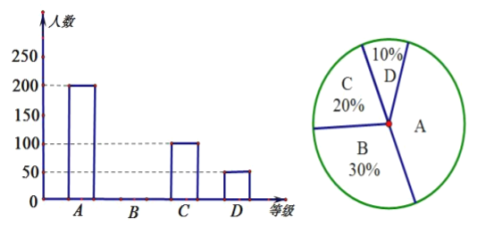
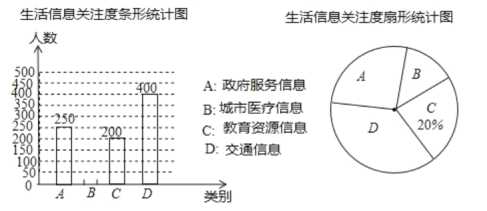
阅读快车系列答案【题目】党的十八大以来,全国各地认真贯彻精准扶贫方略,扶贫工作力度、深度和精准度都达到了新的水平,为2020年全面建成小康社会的战略目标打下了坚实基础.以下是根据近几年中国农村贫困人口数量(单位:万人)及分布情况绘制的统计图表的一部分.
年份 人数 地区 | 2017 | 2018 | 2019 |
东部 | 300 | 147 | 47 |
中部 | 1112 | 181 | |
西部 | 1634 | 916 | 323 |
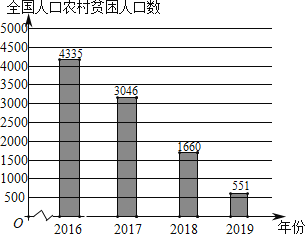
(以上数据来源于国家统计局)
根据统计图表提供的信息,下面推断不正确的是( )
A.2018年中部地区农村贫困人口为597万人
B.2017﹣2019年,农村贫困人口数量都是东部最少
C.2016﹣2019年,农村贫困人口减少数量逐年增多
D.2017﹣2019年,虽然西部农村贫困人口减少数量最多,但是相对于东、中部地区,它的降低率最低