题目内容
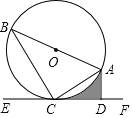
【题目】如图,⊙O是Rt△ABC的外接圆,直径AB=4,直线EF经过点C,AD⊥EF于点D,∠ACD=∠B.
(1)求证:EF是⊙O的切线;
(2)若AD=1,求BC的长;
(3)在(2)的条件下,求图中阴影部分的面积.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)连接OC,由OB=OC,利用等边对等角得到∠BCO=∠B,由∠ACD=∠B,得到∠ACD+∠OCA=90°,即可得到EF为圆O的切线;
(2)证明Rt△ABC∽Rt△ACD,可求出AC=2,由勾股定理求出BC的长即可;
(3)求出∠B=30°,可得∠AOC=60°,在Rt△ACD中,求出CD,然后用梯形ADCO和扇形OAC的面积相减即可得出答案.
(1)证明:连接OC,
∵AB是⊙O直径,
∴∠ACB=90°,即∠BCO+∠OCA=90°,
∵OB=OC,
∴∠BCO=∠B,
∵∠ACD=∠B,
∴∠ACD+∠OCA=90°,
∵OC是⊙O的半径,
∴EF是⊙O的切线;
(2)解:在Rt△ABC和Rt△ACD中,
∵∠ACD=∠B,∠ACB=∠ADC,
∴Rt△ABC∽Rt△ACD,
∴![]() ,
,
∴AC2=ADAB=1×4=4,
∴AC=2,
∴![]() ;
;
(3)解:∵在Rt△ABC中,AC=2,AB=4,
∴∠B=30°,
∴∠AOC=60°,
在Rt△ADC中,∠ACD=∠B=30°,AD=1,
∴CD=![]() =
=![]() =
=![]() ,
,
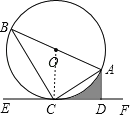
∴S阴影=S梯形ADCO﹣S扇形OAC=![]() .
.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目