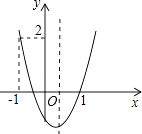题目内容
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作EF⊥AC于点E,交AB的延长线于点F.
(1)求证:EF是⊙O的切线;
(2)如果∠A=60°,则DE与DF有何数量关系?请说明理由;
(3)如果AB=5,BC=6,求tan∠BAC的值.
【答案】
(1)
证明:连接OD,

∵AB=AC,∴∠2=∠C,
∵OD=OB,∴∠2=∠1,
∴∠1=∠C,
∴OD∥AC,
∵EF⊥AC,
∴OD⊥EF,
∵点D在⊙O上,
∴EF是⊙O的切线;
(2)
解:DE与DF的数量关系是DF=2DE.连接AD,
∵AB是⊙O的直径,
∴AD⊥BC,
∵AB=AC,∴∠3=∠4= ![]() ∠BAC=
∠BAC= ![]() ×60°=30°,
×60°=30°,
∵∠F=90°﹣∠BAC=90°﹣60°=30°,
∴∠3=∠F,∴AD=DF,
∵∠4=30°,EF⊥AC,
∴DE= ![]() AD,∴DF=2DE;
AD,∴DF=2DE;
(3)
解:设⊙O与AC的交点为P,连接BP,

∵AB为直径,∴BP⊥AC,由上知BD= ![]() BC=
BC= ![]() ×6=3,
×6=3,
∴AD= ![]() =4,
=4,
S△ABC= ![]() BCAD=
BCAD= ![]() ACBP,
ACBP,
∴ ![]() ×6×4=
×6×4= ![]() ×5×BP,
×5×BP,
∴BP= ![]() ,
,
∴直角△ABP中,AP= ![]() =
= ![]() ,
,
∴tan∠BAC= ![]() =
= ![]() .
.
【解析】(1)连接OD,根据题意可得出∠1=∠C,则OD∥AC,由EF⊥AC可得出结论;(2)连接AD,由圆周角定理可得出AD⊥BC,根据已知条件可得出∠3=30°,从而得出∠3=∠F,则AD=DF,由直角三角形的性质即可得出DF=2DE;(3)设⊙O与AC的交点为P,连接BP,可求出BD,再根据勾股定理求出AD,根据三角形的面积公式得出BP,再由勾股定理得出AP,则得出tan∠BAC的值.
【考点精析】掌握圆的定义和圆周角定理是解答本题的根本,需要知道平面上到定点的距离等于定长的所有点组成的图形叫做圆.定点称为圆心,定长称为半径;顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半.

【题目】在某项针对18~35岁的青年人每天发微博数量的调查中,设一个人的“日均发微博条数”为m,规定:当m≥10时为A级,当5≤m<10时为B级,当0≤m<5时为C级.现随机抽取30个符合年龄条件的青年人开展每人“日均发微博条数”的调查,所抽青年人的“日均发微博条数”的数据如下表:
11 | 10 | 6 | 15 | 9 | 16 | 13 | 12 | 0 | 8 |
2 | 8 | 10 | 17 | 6 | 13 | 7 | 5 | 7 | 3 |
12 | 10 | 7 | 11 | 3 | 6 | 8 | 14 | 15 | 12 |
(1)求样本数据中为A级的频率;
(2)试估计1000个18~35岁的青年人中“日均发微博条数”为A级的人数;
(3)从样本数据为C级的人中随机抽取2人,用列举法求抽得2个人的“日均发微博条数”都是3的概率.