题目内容
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作⊙O的切线DE,交AC于点E,AC的反向延长线交⊙O于点F. 
(1)求证:DE⊥AC;
(2)若DE+EA=8,⊙O的半径为10,求AF的长度.
【答案】
(1)证明:∵OB=OD,
∴∠ABC=∠ODB,
∵AB=AC,
∴∠ABC=∠ACB,
∴∠ODB=∠ACB,
∴OD∥AC.
∵DE是⊙O的切线,OD是半径,
∴DE⊥OD,
∴DE⊥AC;
(2)解:如图,过点O作OH⊥AF于点H,则∠ODE=∠DEH=∠OHE=90°,
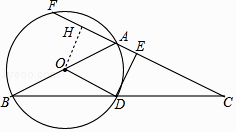
∴四边形ODEH是矩形,
∴OD=EH,OH=DE.
设AH=x.
∵DE+AE=8,OD=10,
∴AE=10﹣x,OH=DE=8﹣(10﹣x)=x﹣2.
在Rt△AOH中,由勾股定理知:AH2+OH2=OA2,即x2+(x﹣2)2=102,
解得x1=8,x2=﹣6(不合题意,舍去).
∴AH=8.
∵OH⊥AF,
∴AH=FH= ![]() AF,
AF,
∴AF=2AH=2×8=16.
【解析】(1)欲证明DE⊥AC,只需推知OD∥AC即可;(2)如图,过点O作OH⊥AF于点H,构建矩形ODEH,设AH=x.则由矩形的性质推知:AE=10﹣x,OH=DE=8﹣(10﹣x)=x﹣2.在Rt△AOH中,由勾股定理知:x2+(x﹣2)2=102 , 通过解方程得到AH的长度,结合OH⊥AF,得到AF=2AH=2×8=16.
【考点精析】通过灵活运用等腰三角形的性质和勾股定理的概念,掌握等腰三角形的两个底角相等(简称:等边对等角);直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2即可以解答此题.

练习册系列答案
相关题目




