题目内容
【题目】如图,△ABC是⊙O的内接三角形,AB是⊙O的直径,OF⊥AB,交AC于点F,点E在AB的延长线上,射线EM经过点C,且∠ACE+∠AFO=180°.
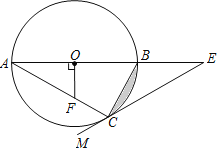
(1)求证:EM是⊙O的切线;
(2)若∠A=∠E,⊙O的半径为1,求阴影部分的面积.
【答案】(1)见解析;(2)![]()
【解析】
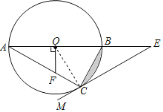
(1)如下图,根据垂径定理得∠AOF=90°,根据三角形内角和得到∠A+∠AFO=90°,根据等腰三角形的性质得到∠OCE=90°,从而证切线;
(2)根据圆周角定理得到∠ACB=90°,推出∠ACO=∠BCE,得到△BOC是等边三角形,根据扇形和等边三角形的面积公式即可得到结论.
解:(1)连接OC,
∵OF⊥AB,
∴∠AOF=90°,
∴∠A+∠AFO=90°,
∵∠ACE+∠AFO=180°,∠ACE+∠ACM=180°
∴.∠AFO=∠ACM
∵OA=OC,
∴∠A=∠ACO,
∴∠ACO+∠ACM.=90°,
∴∠OCM=90°
∴OC⊥ME,
∴EM是⊙O的切线;
(2)∵∠EOC=2∠A=2∠E
又∵∠EOC+∠E=∠COM=90°,
∴∠E+2∠E=90°,
∴∠E=30°,
∴∠EOC=60°,
∴CE=OCtan60°=![]() ,△OCB是等边三角形
,△OCB是等边三角形
∴阴影部分的面积=![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目