题目内容
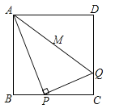
【题目】正方形ABCD的边长为4,P 为BC上的动点,连接PA,作PQ⊥PA,PQ交CD于Q,连接AQ ,则AQ的最小值是( )
A.5B.![]() C.
C.![]() D.4
D.4
【答案】A
【解析】
设BP=x,CQ=y,根据△ABP∽△PCQ可得y关于x的二次函数,利用二次函数的性质,求得y的最大值情况,则QD最小,则AQ最小.
∵四边形ABCD是正方形,
∴∠B=∠C=90°,
∵PQ⊥AP,
∴∠APB+∠QPC=90°,
∠APB+∠BAP=90°,
∴∠BAP=∠QPC,
∴△ABP∽△PCQ,
∴![]() ,
,
设BP=x,CQ=y
即![]() ,
,
∴y=﹣![]() +x=﹣
+x=﹣![]() +1(0<x<4),
+1(0<x<4),
∵﹣![]() <0,
<0,
∴y有最大值,
∴当x=2时,y有最大值1cm.此时QD=3
在Rt△AQP中,![]()
故AQ的最小值是5
故选:A.

【题目】一般地,对于已知一次函数y1=ax+b,y2=cx+d(其中a,b,c,d为常数,且ac<0),定义一个新函数y=![]() ,称y是y1与y2的算术中项,y是x的算术中项函数.
,称y是y1与y2的算术中项,y是x的算术中项函数.
(1)如:一次函数y1=![]() x﹣4,y2=﹣
x﹣4,y2=﹣![]() x+6,y是x的算术中项函数,即y=
x+6,y是x的算术中项函数,即y=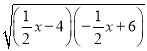 .
.
①自变量x的取值范围是 ,当x= 时,y有最大值;
②根据函数研究的途径与方法,请填写下表,并在图1中描点、连线,画出此函数的大致图象;
x | 8 | 9 | 10 | 12 | 13 | 14 | 16 | 17 | 18 |
y | 0 | 1.2 | 1.6 |
| 2.04 | 2 |
| 1.2 | 0 |
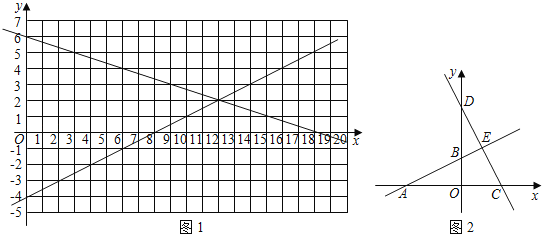
③请写出一条此函数可能有的性质 ;
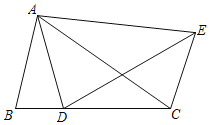
(2)如图2,已知一次函数y1=![]() x+2,y2=﹣2x+6的图象交于点E,两个函数分别与x轴交于点A,C,与y轴交于点B,D,y是x的算术中项函数,即y=
x+2,y2=﹣2x+6的图象交于点E,两个函数分别与x轴交于点A,C,与y轴交于点B,D,y是x的算术中项函数,即y=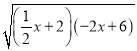 .
.
①判断:点A、C、E是否在此算术中项函数的图象上;
②在平面直角坐标系中是否存在一点,到此算术中项函数图象上所有点的距离相等,如果存在,请求出这个点;如果不存在,请说明理由.
【题目】某校兴趣小组以问卷调查的形式,随机调查了某地居民对武汉封城后续措施的了解情况,设置了多选题,并将调查结果绘制成如图不完整的统计图.
选项 | A | B | C | D | E |
后续措施 | 扩大宣传力度 | 分类隔离病人 | 封闭小区 | 聘请专业物资 | 采取其他措施 |
选择人次 | 25 | 85 | 15 | 35 |
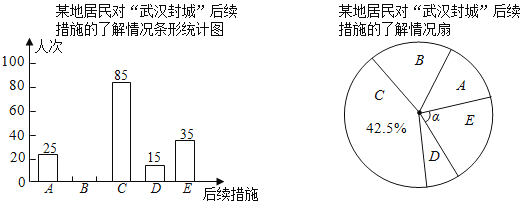
已知平均每人恰好选择了两个选项,根据以上信息回答下列问题:
(1)求参与本次问卷调查的居民人数,并补全条形统计图;
(2)在扇形统计图中,求E选项对应圆心角α的度数;
(3)根据此次调查结果估计该地100万居民当中选择D选项的人数.
【题目】抛物线y=﹣x2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表所示:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | 0 | 4 | 6 | 6 | 4 | … |
从上表可知,下列说法中,错误的是( )
A. 抛物线于x轴的一个交点坐标为(﹣2,0)
B. 抛物线与y轴的交点坐标为(0,6)
C. 抛物线的对称轴是直线x=0
D. 抛物线在对称轴左侧部分是上升的