题目内容
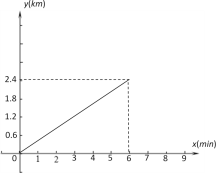
【题目】已知A、B两地相距2.4km,甲骑车匀速从A地前往B地,如图表示甲骑车过程中离A地的路程y(km)与他行驶所用的时间x(min)之间的关系.根据图像解答下列问题:
(1)甲骑车的速度是 km/min;
(2)若在甲出发时,乙在甲前方0.6km处,两人均沿同一路线同时出发匀速前往B地,在第3分钟甲追上了乙,两人到达B地后停止.请在下面同一平面直角坐标系中画出乙离A地的距离y乙(km)与所用时间x(min)的关系的大致图像;
(3)乙在第几分钟到达B地?
(4)两人在整个行驶过程中,何时相距0.2km?
【答案】(1)0.4(2)见解析(3)9分钟 (4)2分钟,4分钟,8分钟.
【解析】
(1)根据速度等于路程除以时间进行解答即可;
(2)根据“在甲出发时,乙在甲前方0.6km处”可知过点(0,0.6),根据“在第3分钟甲追上了乙”可知该图像过横坐标为3的点,过着两点即可画出;
(3)求出y甲=0.4x,把x=3代入y=0.4x,求得y=1.2,再求出 y乙=0.2x+0.6,把y=2.4代入y乙=0.2x+0.6得x=9,所以乙在第9分钟到达B地;
(4)分三种情况,相遇前,相遇后和甲到达后相距0.2km.
解:(1)0.4,
(2)如图:
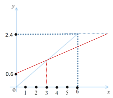
(3)设甲的函数的表达式为y甲=kx,然后把x=6,y=2.4代入求得k=0.4,所以函数表达式为y甲=0.4x,把x=3代入y=0.4x,求得y=1.2,
设乙的函数表达式为y乙=kx+b,然后把x=0,y=0.6;x=3,y=1.2分别代入
求得k=0.2,b=0.6,所以函数表达式为y乙=0.2x+0.6,
把y=2.4代入y乙=0.2x+0.6得x=9,
所以乙在第9分钟到达B地.
(4)①相遇前是y乙-y甲=0.2即0.2x+0.6-0.4x=0.2,解得x=2,
所以在第2分钟两人相距0.2km;
②相遇后是y甲-y乙=0.2即0.4x-(0.2x+0.6)=0.2,解得x=4,
所以在第4分钟两人相距0.2km.
③把y=2.2代入y乙=0.2x+0.6得x=8,
所以第8分钟时两人相距0.2km.