ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒxOy÷–(»γΆΦ)Θ§“―÷Σ≈ΉΈοœΏyΘΫ©¹![]() +bx+c(Τδ÷–bΓΔc «≥Θ ΐ)Ψ≠ΙΐΒψA(©¹2Θ§©¹2)”κΒψB(0Θ§4)Θ§ΕΞΒψΈΣMΘ°
+bx+c(Τδ÷–bΓΔc «≥Θ ΐ)Ψ≠ΙΐΒψA(©¹2Θ§©¹2)”κΒψB(0Θ§4)Θ§ΕΞΒψΈΣMΘ°
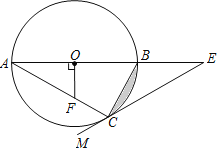
Θ®1Θ©«σΗΟ≈ΉΈοœΏΒΡ±μ¥ο Ϋ”κΒψMΒΡΉχ±ξΘΜ
Θ®2Θ©ΤΫ“Τ’βΧθ≈ΉΈοœΏΘ§ΒΟΒΫΒΡ–¬≈ΉΈοœΏ”κy÷αΫΜ”ΎΒψC(ΒψC‘ΎΒψBΒΡœ¬ΖΫ)Θ§«“ΓςBCMΒΡΟφΜΐΈΣ3Θ°–¬≈ΉΈοœΏΒΡΕ‘≥Τ÷αlΨ≠ΙΐΒψAΘ§÷±œΏl”κx÷αΫΜ”ΎΒψDΘ°
ΔΌ«σΒψAΥφ≈ΉΈοœΏΤΫ“ΤΚσΒΡΕ‘”ΠΒψΉχ±ξΘΜ
ΔΎΒψEΓΔG‘Ύ–¬≈ΉΈοœΏ…œΘ§«“ΙΊ”Ύ÷±œΏlΕ‘≥ΤΘ§»γΙϊ’ΐΖΫ–ΈDEFGΒΡΕΞΒψF‘ΎΒΎΕΰœσœόΡΎΘ§«σΒψFΒΡΉχ±ξΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() ΘΜΕΞΒψMΒΡΉχ±ξ «ΘΚ(2Θ§6)ΘΜΘ®2Θ©ΔΌΒψAΕ‘”ΠΒψΒΡΉχ±ξΈΣ(©¹6Θ§©¹5)ΘΜΔΎF(©¹2Θ§
ΘΜΕΞΒψMΒΡΉχ±ξ «ΘΚ(2Θ§6)ΘΜΘ®2Θ©ΔΌΒψAΕ‘”ΠΒψΒΡΉχ±ξΈΣ(©¹6Θ§©¹5)ΘΜΔΎF(©¹2Θ§![]() )Θ°
)Θ°
ΓΨΫβΈωΓΩ
Θ®1Θ©ΗυΨί≈ΉΈοœΏyΘΫ©¹![]() +bx+c(Τδ÷–bΓΔc «≥Θ ΐ)Ψ≠ΙΐΒψA(©¹2Θ§©¹2)”κΒψB(0Θ§4)Θ§¥”ΕχΩ…“‘«σΒΟ≈ΉΈοœΏΒΡΫβΈω ΫΘ§»ΜΚσΫΪΫβΈω ΫΜ·ΈΣΕΞΒψ ΫΘ§Φ¥Ω…ΒΟΒΫΕΞΒψMΒΡΉχ±ξΘΜ
+bx+c(Τδ÷–bΓΔc «≥Θ ΐ)Ψ≠ΙΐΒψA(©¹2Θ§©¹2)”κΒψB(0Θ§4)Θ§¥”ΕχΩ…“‘«σΒΟ≈ΉΈοœΏΒΡΫβΈω ΫΘ§»ΜΚσΫΪΫβΈω ΫΜ·ΈΣΕΞΒψ ΫΘ§Φ¥Ω…ΒΟΒΫΕΞΒψMΒΡΉχ±ξΘΜ
Θ®2Θ©ΔΌΗυΨί–¬≈ΉΈοœΏΒΡΕ‘≥Τ÷αlΨ≠ΙΐΒψAΘ§Ω…ΒΟ–¬≈ΉΈοœΏΒΡΕΞΒψΈΣ(-2,k)Θ§…ηΤΫ“ΤΚσ–¬≈ΉΈοœΏΒΡΫβΈω ΫΈΣ![]() Θ§Ω…ΒΟCΒψΉχ±ξΘ§”…ΟφΜΐΝ–ΖΫ≥Χ«σ≥ωkΘ§¥”ΕχΩ…“‘ΒΟΒΫΒψAΥφ≈ΉΈοœΏΤΫ“ΤΚσΒΡΕ‘”ΠΒψΉχ±ξΘΜ
Θ§Ω…ΒΟCΒψΉχ±ξΘ§”…ΟφΜΐΝ–ΖΫ≥Χ«σ≥ωkΘ§¥”ΕχΩ…“‘ΒΟΒΫΒψAΥφ≈ΉΈοœΏΤΫ“ΤΚσΒΡΕ‘”ΠΒψΉχ±ξΘΜ
ΔΎΗυΨίΧβ“βΚΆ’ΐΖΫ–ΈΒΡ–‘÷ Θ§…ηF(©¹2Θ§2a)ΓΔE(©¹2+aΘ§a)Θ°ΫΪE¥ζ»κΘ®2Θ©ΒΡΫβΈω Ϋ÷–Φ¥Ω…«σ≥ωaΘ§ΦΧΕχΫβΧβΘ°Ω…“‘«σΒΟΒψFΒΡΉχ±ξΘ°
ΫβΘΚΘ®1Θ©ΫΪA(©¹2Θ§©¹2)ΓΔB(0Θ§4)¥ζ»κ![]() ÷–Θ§
÷–Θ§
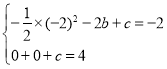
ΫβΒΟ![]()
ΓύΗΟ≈ΉΈοœΏΒΡ±μ¥ο ΫΈΣΘΚ![]() ΘΜ
ΘΜ
ΓΏyΘΫ![]() x2+2x+4ΘΫ
x2+2x+4ΘΫ![]() (x©¹2)2+6Θ§
(x©¹2)2+6Θ§
ΓύΕΞΒψMΒΡΉχ±ξ «ΘΚ(2Θ§6)ΘΜ
Θ®2Θ©ΔΌΓΏΤΫ“ΤΚσ≈ΉΈοœΏΒΡΕ‘≥Τ÷αΨ≠ΙΐΒψA(©¹2Θ§©¹2)Θ§
ΓύΩ……ηΤΫ“ΤΚσΒΡ≈ΉΈοœΏ±μ¥ο ΫΈΣΘΚ![]() Θ§
Θ§
ΓύC(0Θ§©¹2+k)Θ°
Γύ![]() Θ§
Θ§
ΫβΒΟΘ§kΘΫ3Θ°
Γύ![]() Θ§
Θ§
Φ¥‘≠≈ΉΈοœΏœρΉσΤΫ“Τ4ΗωΒΞΈΜΘ§œρœ¬ΤΫ“Τ3ΗωΒΞΈΜΩ…“‘ΒΟΒΫ–¬ΒΡ≈ΉΈοœΏΘ°
ΓύΒψAΕ‘”ΠΒψΒΡΉχ±ξΈΣ(©¹6Θ§©¹5)ΘΜ
ΔΎ…ηEG”κDFΒΡΫΜΒψΈΣHΘ° ‘Ύ’ΐΖΫ–ΈDEFG÷–Θ§EGΓΆDFΘ§EGΘΫDFΘΫ2EHΘΫ2DHΘ°
ΓΏΒψEΓΔG «’βΧθ≈ΉΈοœΏ…œΒΡ“ΜΕ‘Ε‘≥ΤΒψΘ§
ΓύEGΓΈx÷αΘ°
ΓύDFΓΆx÷αΘ§
…ηF(©¹2Θ§2a)Θ°
ΓΏΒψF‘ΎΒΎΕΰœσœόΡΎΘ§
ΓύaΘΨ0Θ°
ΓύEGΘΫDFΘΫ2EHΘΫ2DHΘΫ2aΘ°
≤ΜΖΝ…ηΒψE‘ΎΒψGΒΡ”“≤ύΘ§Ρ«Ο¥E(©¹2+aΘ§a)Θ°
ΫΪΒψE¥ζ»κ![]() Θ§ΒΟ
Θ§ΒΟ![]() Θ§
Θ§
ΫβΒΟΘ§![]() Θ§
Θ§![]() (≤ΜΚœΧβ“βΘ§…α»Ξ)Θ°
(≤ΜΚœΧβ“βΘ§…α»Ξ)Θ°
ΓύF(©¹2Θ§![]() )Θ°
)Θ°

 ‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ