��Ŀ����
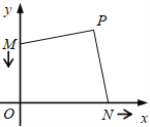
����Ŀ������ij����ʵʩ��ҵ����ƶ������ƶ�����а�������Ķ������ֲ��Ʒ��ݮ����֪�ò�ݮ�ijɱ�Ϊÿǧ��10Ԫ����ݮ�����Ͷ���г����ۣ����г����鷢�֣���ݮ���۲����������ÿ���������y��ǧ�ˣ������۵���x��Ԫ/ǧ�ˣ�֮�亯����ϵ��ͼ��ʾ��
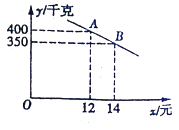
��1����y��x�ĺ�����ϵʽ����д��x��ȡֵ��Χ��
��2������Ʒ�ֲ�ݮ�Ķ���Ϊ����ʱ��ÿ�����ۻ�����������������Ƕ��٣�
��3��ij������ݮ��ժ����30�죬Ԥ�Ʋ���6000ǧ�ˣ����գ�2���еķ�ʽ�������ۣ��ܷ�������������ݮ����˵�����ɣ�
���𰸡���1��y=-25x+700��10��x��28������2����Ʒ�ֲ�ݮ����Ϊ19Ԫ/ǧ��ʱ��ÿ�����ۻ�õ��������Ϊ2025Ԫ����3����������������ݮ�����ɼ�������
��������
��1�����ô���ϵ�������ɵý��ۣ�
��2�����ݡ�������=������������������г���������ʽ�����䷽�ɶ���ʽ���ɵó����ֵ��
��3������ڣ�2��������£���x=19ʱÿ������������ݴ����30��������������Ƚϼ��ɵó��𰸣�
��1����y��x�ĺ�����ϵʽΪy=kx+b��k��0������A��12��400����B��14��350���ֱ�����![]() ����ã�
����ã�![]() ����y��x�ĺ�����ϵʽΪy=-25x+700��������֪��
����y��x�ĺ�����ϵʽΪy=-25x+700��������֪��![]() ����10��x��28��
����10��x��28��
��2����ÿ�����������ΪwԪ��������֪w=��x-10����-25x+700��=-25x2+950x-7000 =-25��x-19��2+2025��
��a=-25��0���൱x=19ʱ��wȡ���ֵ��Ϊ2025��
����Ʒ�ֲ�ݮ����Ϊ19Ԫ/ǧ��ʱ��ÿ�����ۻ�õ��������Ϊ2025Ԫ��
��3����������������ݮ���������£�
��x=19ʱ��y=-25��19+700=225��225��30=6750��6000��
�ఴ�գ�2���еķ�ʽ�������ۣ��������꣮

 ǧ�������������ĩ�����Ծ�����ϵ�д�
ǧ�������������ĩ�����Ծ�����ϵ�д�����Ŀ��������y=��x2+bx+c�ϲ��ֵ�ĺ�����x��������y�Ķ�Ӧֵ���±���ʾ��
x | �� | ��2 | ��1 | 0 | 1 | 2 | �� |
y | �� | 0 | 4 | 6 | 6 | 4 | �� |
���ϱ���֪������˵���У�������ǣ� ��
A. ��������x���һ����������Ϊ����2��0��
B. ��������y��Ľ�������Ϊ��0��6��
C. �����ߵĶԳ�����ֱ��x=0
D. �������ڶԳ�����ಿ����������