Question

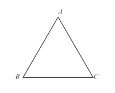
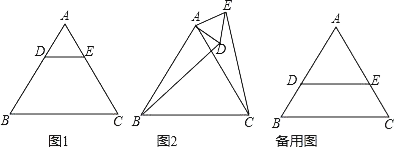
【题目】问题发现：如图1，△ABC是等边三角形，点D是边AD上的一点，过点D作DE∥BC交AC于E，则线段BD与CE有何数量关系？

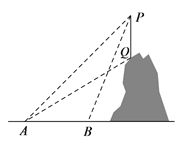
拓展探究：如图2，将△ADE绕点A逆时针旋转角α（0°＜α＜360°），上面的结论是否仍然成立？如果成立，请就图中给出的情况加以证明．

问题解决：如果△ABC的边长等于2，AD＝2，直接写出当△ADE旋转到DE与AC所在的直线垂直时BD的长．

Answer 1

【答案】问题发现：BD＝CE；拓展探究：结论仍然成立，见解析；问题解决：BD的长为2和2．

【解析】

问题发现：如图1，由平行线分线段成比例定理可得BD＝CE；

拓展探究：如图2，证明△BAD≌△CAE，可得BD＝CE；

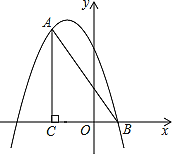
问题解决：分两种情况：①如图3，在直角三角形中，根据30°角所对的直角边等于斜边的一半求出DG＝1，由勾股定理求出AG＝，得出BG，从而计算出BD的长．

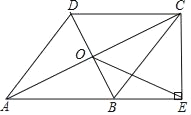
②如图4，求EF的长和CF的长，根据勾股定理在Rt△EFC中求EC的长，所以BD＝EC＝2．

解: 问题发现：如图1,BD=CE,理由是

∵△ABC是等边三角形,

∴AB=AC,

∵DE∥BC,

∴BD=CE,
拓展探究：结论仍然成立,如图2,
由图1得,△ADE是等边三角形,

∴AD=AE,
由旋转得∠BAD=∠CAE,△BAD≌△CAE,(旋转的性质)
∴BD=CE,
问题解决：当△ADE旋转到DE与AC所在的直线垂直时,设垂足为点F,此时有两种情况:

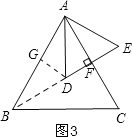
①如图3,

∵△ADE是等边三角形,AF⊥DE,

∴∠DAF=∠EAF=30°,
∴∠BAD=30°,
过D作DG⊥AB,垂足为G,

∵AD=2,
∴DG=1,AG=,

∵AB=2,
∴BG=AB-AG=,
∴BD=2（勾股定理）,
②如图4,

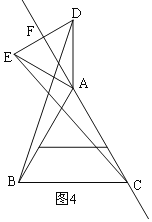
同理得△BAD≌△CAE,

∴BD=CE,
∵△ADE是等边三角形,

∴∠ADE=60°,
∵AD=AE,DE⊥AC,
∴∠DAF=∠EAF=30°,
∴EF=FD=AD=1,

∴AF=,
∴CF=AC+CF=2+=3,

在Rt△EFC中,EC=,

∴BD=EC=2.

综上所述,BD的长为2和2.