题目内容
【题目】如图所示,某教学活动小组选定测量小山上方某信号塔PQ的高度,他们在A处测得信号塔顶端P的仰角为45°,信号塔低端Q的仰角为31°,沿水平地面向前走100米到处,测得信号塔顶端P的仰角为68°.求信号塔PQ的高度.(结果精确到0.1米.参考数据:sin68°≈ 0.93,cos68° ≈ 0.37,tan68° ≈ 2.48,tan31° ≈ 0.60,sin31° ≈ 0.52,cos31°≈0.86)
【答案】信号塔PQ的高度约为67.0米
【解析】延长PQ交直线AB于点E,连接AQ,设PM的长为x米,先由三角函数得出方程求出PM,再由三角函数求出QM,得出PQ的长度即可.
解:延长PQ交直线AB于点M,
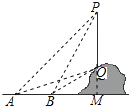
则∠PMA=90°,设PM的长为x米,根据题意,
得∠PAM=45°,∠PBM=68°,∠QAM=31°,
AB=100,∴在Rt△PAM中,AM=PM=x.
BM=AM-AB=x-100,
在Rt△PBM中,∵tan∠PBM=![]() ,
,
即tan68°=![]() .
.
解得x ≈ 167.57.∴AM=PM ≈ 167.57.
在Rt△QAM中,∵tan∠QAM=![]() ,
,
∴QM=AM·tan∠QAM=167.57×tan31°≈100.54.
∴PQ=PM-QM=167.57-100.54≈67.0(米).
因此,信号塔PQ的高度约为67.0米.
“点睛”本题考查直角三角形的应用、三角函数;由三角函数得出方程是解决问题的关键,注意掌握当两个直角三角形有公共边时,先求出这条公共边的边长是解答此类题的一般思路.

练习册系列答案
相关题目