题目内容
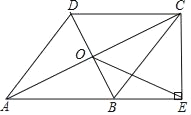
【题目】如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E,连接OE.
(1)求证:四边形ABCD是菱形;
(2)若AB=![]() ,BD=2,求OE的长.
,BD=2,求OE的长.
【答案】(1)见解析;(2)OE=2.
【解析】
(1)先判断出∠OAB=∠DCA,进而判断出∠DAC=∠DAC,得出CD=AD=AB,即可得出结论;
(2)先判断出OE=OA=OC,再求出OB=1,利用勾股定理求出OA,即可得出结论.
解:(1)∵AB∥CD,
∴∠OAB=∠DCA,
∵AC为∠DAB的平分线,
∴∠OAB=∠DAC,
∴∠DCA=∠DAC,
∴CD=AD=AB,
∵AB∥CD,
∴四边形ABCD是平行四边形,
∵AD=AB,
∴ABCD是菱形;
(2)∵四边形ABCD是菱形,
∴OA=OC,BD⊥AC,∵CE⊥AB,
∴OE=OA=OC,
∵BD=2,
∴OB=![]() BD=1,
BD=1,
在Rt△AOB中,AB=![]() ,OB=1,
,OB=1,
∴OA=![]() =2,
=2,
∴OE=OA=2.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
【题目】某校组织七年级学生体育健康抽测,(1)班25名学生的成绩(满分为100分)统计如下:
90,74,88,65,98,76,81,42,85,70,55,80,95,88,72,87,61,56,76,66,78,72,82,63,100.
(1)90分及以上为A级,75-89分为B级,60-74分为C级,60分以下为D级,请把下面表格补充完整,并将图中的条形图补充完整;
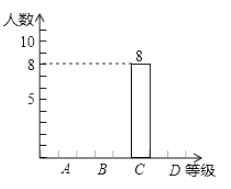
等级 | A | B | C | D |
人数 | 8 |
(2)该校七年级共有1000名学生,如果60分以上为合格,请估计七年级有多少人合格?
(3)请选择合适的统计图表示出抽测中每一个等级的人数占总人数的百分比.