��Ŀ����
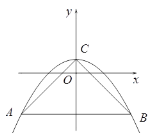
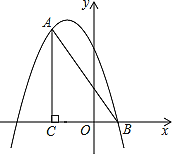
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���ACB=90�㣬OC=2OB��tan��ABC=2����B������Ϊ��1��0����������y=��x2+bx+c����A��B���㣮
��1���������ߵĽ���ʽ��
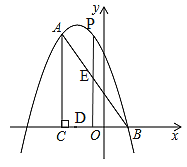
��2����P��ֱ��AB�Ϸ��������ϵ�һ�㣬����P��PD��ֱx���ڵ�D�����߶�AB�ڵ�E��ʹPE=![]() DE��
DE��
�����P�����ꣻ
����ֱ��PD���Ƿ���ڵ�M��ʹ��ABMΪֱ�������Σ������ڣ�����������������е�M�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��y=��x2��3x+4����2����P����1��6�����ڴ��ڣ�M����1��3+![]() ����1��3��
����1��3��![]() ����1����1����1��
����1����1����1��![]() ����
����
��������
��1���ȸ�����֪���A�����꣬���ô���ϵ��������κ����Ľ���ʽ��
��2�����ȵ�AB�Ľ���ʽΪ��y=-2x+2������PD��x�ᣬ��P��x��-x2-3x+4������E��x��-2x+2��������PE=![]() DE���з��̿ɵ�P�����ꣻ
DE���з��̿ɵ�P�����ꣻ
�������M�����꣬����������빫ʽ�ɵ�AB��AM��BM�ij����������������ABMΪֱ��������ʱ���ֱ���A��B��MΪֱ�Ƕ���ʱ�����ù��ɶ����з��̿ɵõ�M�����꣮
�⣺��1����B��1��0������OB=1��
��OC=2OB=2����C����2��0����
Rt��ABC��tan��ABC=2��
��![]() �� ��
�� ��![]() �� ��AC=6��
�� ��AC=6��
��A����2��6����
��A����2��6����B��1��0������y=��x2+bx+c�ã�![]() ��
��
��ã�![]() ��
��
�������ߵĽ���ʽΪ��y=��x2��3x+4��
��2���١�A����2��6����B��1��0����
��AB�Ľ���ʽΪ��y=��2x+2��
��P��x����x2��3x+4������E��x����2x+2����
��PE=![]() DE��
DE��
�ੁx2��3x+4������2x+2��=![]() ����2x+2����
����2x+2����
��x=-1��1���ᣩ��
��P����1��6����
�ڡ�M��ֱ��PD�ϣ���P����1��6����
��M����1��y����
��B��1��0����A����2��6��
��AM2=����1+2��2+��y��6��2=1+��y��6��2��
BM2=��1+1��2+y2=4+y2��
AB2=��1+2��2+62=45��
�����������
i������AMB=90��ʱ����AM2+BM2=AB2��
��1+��y��6��2+4+y2=45��
��ã�y=3![]() ��
��
��M����1��3+![]() ����1��3��
����1��3��![]() ����
����
ii������ABM=90��ʱ����AB2+BM2=AM2��
��45+4+y2=1+��y��6��2�� ��y=��1��
��M����1����1����
iii������BAM=90��ʱ����AM2+AB2=BM2��
��1+��y��6��2+45=4+y2�� ��y=![]() ��
��
��M����1��![]() ����
����
������������M����������M����1��3+![]() ����1��3��
����1��3��![]() ����1����1����1��
����1����1����1��![]() ����
����

 ���ſ����ϵ�д�
���ſ����ϵ�д� ���Ŀ����ϵ�д�
���Ŀ����ϵ�д� ������ӱ������ͯ������ϵ�д�
������ӱ������ͯ������ϵ�д� A�ӽ��� ϵ�д�
A�ӽ��� ϵ�д�����Ŀ��ijУ���꼶�ס�������ֱ�ѡ5��ͬѧ�μ���ѧ��������ݽ���������Ԥ���ɼ���ͼ��

��1��������ͼ����±���ȱ���ݣ�
ƽ���� | ��λ�� | ���� | ���� | |
�װ� | 8.5 | 8.5 | ||
�Ұ� | 8 | 10 | 1.6 |
��2�������ϱ��е�ƽ��������λ���ͷ�������Ϊ�İ�ijɼ��Ϻã���˵���������.