题目内容
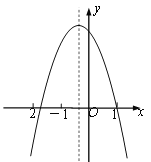
【题目】若二次函数y=ax2+bx+c(a≠0)的图象于x轴的交点坐标分别为(x1,0),(x2,0),且x1<x2,图象上有一点M(x0,y0)在x轴下方,对于以下说法:①b2﹣4ac>0②x=x0是方程ax2+bx+c=y0的解③x1<x0<x2④a(x0﹣x1)(x0﹣x2)<0其中正确的是( )
A.①③④B.①②④C.①②③D.②③
【答案】B
【解析】
①根据二次函数图象与x轴有两个不同的交点,结合根的判别式即可得出△=b2-4ac>0,①正确;②由点M(x0,y0)在二次函数图象上,利用二次函数图象上点的坐标特征即可得出x=x0是方程ax2+bx+c=y0的解,②正确;③分a>0和a<0考虑,当a>0时得出x1<x0<x2;当a<0时得出x0<x1或x0>x2,③错误;④将二次函数的解析式由一般式转化为交点式,再由点M(x0,y0)在x轴下方即可得出y0=a(x0-x1)(x0-x2)<0,④正确.
①∵二次函数y=ax2+bx+c(a≠0)的图象于x轴的交点坐标分别为(x1,0),(x2,0),且x1<x2,
∴方程ax2+bx+c=0有两个不相等的实数根,
∴△=b2-4ac>0,①正确;
②∵图象上有一点M(x0,y0),
∴a![]() +bx0+c=y0,
+bx0+c=y0,
∴x=x0是方程ax2+bx+c=y0的解,②正确;
③当a>0时,∵M(x0,y0)在x轴下方,
∴x1<x0<x2;
当a<0时,∵M(x0,y0)在x轴下方,
∴x0<x1或x0>x2,③错误;
④∵二次函数y=ax2+bx+c(a≠0)的图象于x轴的交点坐标分别为(x1,0),(x2,0),
∴y=ax2+bx+c=a(x-x1)(x-x2),
∵图象上有一点M(x0,y0)在x轴下方,
∴y0=a(x0-x1)(x0-x2)<0,④正确;
故选B.

 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案