题目内容
【题目】（初步认识）
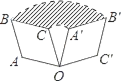
（1）如图，将△ABO绕点O顺时针旋转90°得到△MNO，连接AM、BM，
求证△AOM∽△BON．
（拓展延伸）
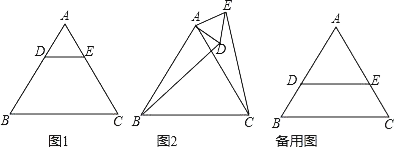
（2）如图，在等边△ABC中，点E在△ABC内部，且满足AE2＝BE2＋CE2，用直尺和圆规作出所有的点E（保留作图的痕迹，不写作法）．
【答案】（1）详见解析；（2）2
【解析】
（1）利用旋转的性质可也得到AO＝OM，BO＝ON，∠AOM＝∠BON＝90°，即可解答
（2）根据题意以AB,AC作为半径做圆，使得B,C两点落在圆上，点E在弧BC上（不包括B,C两点）
（1）证明：∵△ABO绕点O顺时针旋转90°得到△MNO，
∴AO＝OM，
BO＝ON，
∠AOM＝∠BON＝90°．
∵
，
∴△AOM∽△BON．
（2）画图正确
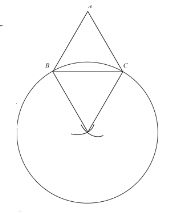
∴点E在弧BC上（不包括B,C两点）
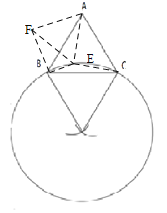
理由要点：（1）将△ACE旋转60°；则∠FAE=60°，AE=AF=EF,EC=FB.
（2）∠BEC＝150°．则可得旋转后∠FBE=90°，则有FB2+EB2=EF2.
练习册系列答案
相关题目
【题目】（某中学九年级学生共600人，其中男生320人，女生280人．该校对九年级所有学生进行了一次体育模拟测试，并随机抽取了部分学生的测试成绩作为样本进行分析，绘制成如下的统计表：
类别 | 成绩（分） | 频数 | 频率 |
I | 40 | 36 | 0.3 |
II | 37—39 | a | b |
III | 34—36 | 24 | 0.2 |
IV | 31—33 | 6 | 0.05 |
合计 | c | 1 | |
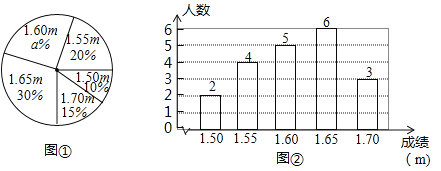
（1）a＝ ； b＝ ；
（2）若将该表绘制成扇形统计图，那么Ⅲ类所对应的圆心角是 °；
（3）若随机抽取的学生中有64名男生和56名女生，请解释“随机抽取64名男生和56名女生”的合理性；
（4）估计该校九年级学生体育测试成绩是40分的人数．
