题目内容
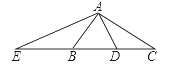
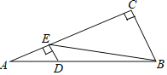
【题目】如图，在△ABC中，∠C=90°，∠A=30°，D为AB上一点，且AD：DB=1：3，DE⊥AC于点E，连接BE，则tan∠CBE的值等于（ ）
A. 
B. 
C. 
D. 
【答案】C
【解析】
根据题意和30°角所对的直角边与斜边的关系，设AB=4a，可以用a分别表示出CE和CB的值，从而可以求得tan∠CBE的值．
设AB=4a，
∵在△ABC中，∠C=90°，∠A=30°，D为AB上一点，且AD：DB=1：3，
∴BC=2a，AC=2
a，AD：AB=1：4，
∵∠C=90°，DE⊥AC，
∴∠AED=90°，
∴∠AED=∠C，
∴DE∥BC，
∴△AED∽△ACB，
∴
，
∴
，
∴AE=
a＝
，
∴EC=AC-AE=2a＝
，
∴tan∠CBE=
，
故选C．
练习册系列答案
新非凡教辅冲刺100分系列答案
相关题目
【题目】吴京同学根据学习函数的经验，对一个新函数
的图象和性质进行了如下探究，请帮他把探究过程补充完整．
（1）该函数的自变量
的取值范围是______．
（2）列表：
| … |
|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
| … |
|
|
|
|
|
|
|
|
| … |
表中
________，
_______．
（3）描点、连线
在下面的格点图中，建立适当的平面直角坐标系
中，描出上表中各对对应值为坐标的点（其中为横坐标，
为纵坐标），并根据描出的点画出该函数的图象：
（4）观察所画出的函数图象，写出该函数的两条性质：
①_______________________________________；
②_______________________________________．
（5）函数与直线
的交点有2个，那么
的取值范围_________．
