��Ŀ����
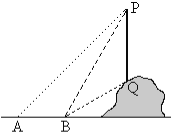
����Ŀ����ͼ��ʾ��ij��ѧ�С��Ҫ����ɽ���ϵĵ��߸�PQ�ĸ߶������Dz�ȡ�ķ����ǣ����ڵ����ϵĵ�A����ø˶��˵�P��������45��������ǰ�ߵ�B������ø˶��˵�P�˵˵�Q�����Ƿֱ���60���30������ʱֻ��Ҫ���AB�ij��Ⱦ���ͨ������������߸�PQ�ĸ߶�����ͬ�����ǵIJ�����������ͬ������������ʱ��ͼ������Ҫд�������˼·�������������ֵ������ͬ���������IJ�������������Ҫд������˼·��
���𰸡�![]() m��
m��
��������
����������ӳ�PQ��ֱ��AB�ڵ�E������AB�ij���Ϊm������ֱ����APE��ֱ����BPE�����������Ǻ�������PE��ʾ��AE��BE������AB=AE-BE�����г��������PE��ֵ������ֱ����BQE���������Ǻ������QE�ij�����PQ�ij��ȼ��������
���������ͬ�����ǵIJ���������
�ӳ�PQ��ֱ��AB�ڵ�E��
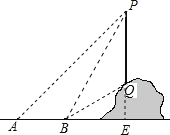
����AB�ij���Ϊm����
��ֱ����APE������A=45����
��AE=PE��
�ߡ�PBE=60��
���BPE=30��
��ֱ����BPE����BE=![]() PE��
PE��
��AB=AE-BE=m��
��PE-![]() PE=m��
PE=m��
��ã�PE=![]() m��
m��
��BE=![]() m-m=
m-m=![]() m��
m��
��ֱ����BEQ����QE=![]() BE=
BE=![]() ��
��![]() m��=
m��=![]() m��
m��
��PQ=PE-QE=![]() m-
m-![]() m=
m=![]() m��
m��

��ϰ��ϵ�д�
�����Ŀ