题目内容
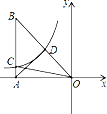
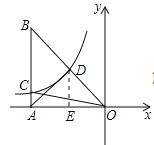
【题目】如图，已知反比函数
的图象过Rt△ABO斜边OB的中点D，与直角边AB相交于C，连结AD、OC，若△ABO的周长为
，AD=2，则△ACO的面积为（ ）
A. 
B. 1 C. 2 D. 4
【答案】A
【解析】
在直角三角形AOB中，由斜边上的中线等于斜边的一半，求出OB的长，根据周长求出直角边之和，设其中一直角边AB=x，表示出OA，利用勾股定理求出AB与OA的长，过D作DE垂直于x轴，得到E为OA中点，求出OE的长，在直角三角形DOE中，利用勾股定理求出DE的长，利用反比例函数k的几何意义求出k的值，确定出三角形AOC面积即可．
在Rt△AOB中，AD=2，AD为斜边OB的中线，
∴OB=2AD=4，
由周长为4+2
，得到AB+AO=2，
设AB=x，则AO=2-x，
根据勾股定理得：AB2+OA2=OB2，即x2+（2-x）2=42，
整理得：x2-2x+4=0，
解得x1=+
，x2=-，
∴AB=+，OA=-，
过D作DE⊥x轴，交x轴于点E，可得E为AO中点，
∴OE=
OA=(-)（假设OA=+，与OA=-，求出结果相同），
在Rt△DEO中，利用勾股定理得：DE=
=(+)），
∴k=-DEOE=-(+)）×(-)）=1.
∴S△AOC=DEOE=，
故选A．
名师指导期末冲刺卷系列答案
【题目】某商家经销一种绿茶，用于装修门面已投资3000元．已知绿茶每千克成本50元，经研究发现销量y（kg）随销售单价x（元/kg）的变化而变化，具体变化规律如表所示：
销售单价x（元/kg） | … | 70 | 75 | 80 | 85 | 90 | … |
月销售量y（kg） | … | 100 | 90 | 80 | 70 | 60 | … |
设该绿茶的月销售利润为w（元）（销售利润＝单价×销售量﹣成本）
（1）请根据上表，写出y与x之间的函数关系式（不必写出自变量x的取值范围）；
（2）求w与x之间的函数关系式（不必写出自变量x的取值范围），并求出x为何值时，w的值最大？
（3）若在第一个月里，按使w获得最大值的销售单价进行销售后，在第二个月里受物价部门干预，销售单价不得高于80元，要想在全部收回装修投资的基础上使第二个月的利润至少达到1700元，那么第二个月时里应该确定销售单价在什么范围内？
