题目内容
【题目】吴京同学根据学习函数的经验，对一个新函数
的图象和性质进行了如下探究，请帮他把探究过程补充完整．
（1）该函数的自变量
的取值范围是______．
（2）列表：
| … |
|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
| … |
|
|
|
|
|
|
|
|
| … |
表中
________，
_______．
（3）描点、连线
在下面的格点图中，建立适当的平面直角坐标系
中，描出上表中各对对应值为坐标的点（其中为横坐标，
为纵坐标），并根据描出的点画出该函数的图象：
（4）观察所画出的函数图象，写出该函数的两条性质：
①_______________________________________；
②_______________________________________．
（5）函数与直线
的交点有2个，那么
的取值范围_________．
【答案】（1）一切实数；（2）
；
；（3）见解析；（4）①该函数有最小值没有最大值；②该函数图象关于直线x=2对称；（5）-5＜m＜0
【解析】
（1）根据分式的分母不等于零，即可求解；
（2）把自变量的值代入即可求解；
（3）根据题意描点、连线即可该函数的图象；
（4）观察图象即可得出该函数的两条性质．
（5）根据函数
与直线
的交点有2个，可得方程
有两个不相等的实数根，利用根的判别式即可求解，也可根据图像解答．
解：（1）由知，x2-4x+5=
≠0，所以变量x的取值范围是一切实数．
故答案为：一切实数；
（2）m= 
＝，n=
＝，
故答案为：；；
（3）建立适当的直角坐标系，描点画出图形，如下图所示：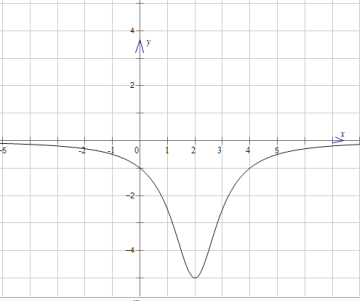
（4）观察所画出的函数图象，有如下性质：
①该函数有最小值没有最大值；
②该函数图象关于直线x=2对称．
故答案为：该函数有最小值没有最大值；该函数图象关于直线x=2对称；
（5）∵函数与直线的交点有2个，
∴方程有两个不相等的实数根，整理方程得：
∴
，即
，解得-5＜m＜0，
∴
的取值范围为：-5＜m＜0．
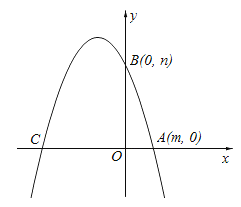
【题目】某商家经销一种绿茶，用于装修门面已投资3000元．已知绿茶每千克成本50元，经研究发现销量y（kg）随销售单价x（元/kg）的变化而变化，具体变化规律如表所示：
销售单价x（元/kg） | … | 70 | 75 | 80 | 85 | 90 | … |
月销售量y（kg） | … | 100 | 90 | 80 | 70 | 60 | … |
设该绿茶的月销售利润为w（元）（销售利润＝单价×销售量﹣成本）
（1）请根据上表，写出y与x之间的函数关系式（不必写出自变量x的取值范围）；
（2）求w与x之间的函数关系式（不必写出自变量x的取值范围），并求出x为何值时，w的值最大？
（3）若在第一个月里，按使w获得最大值的销售单价进行销售后，在第二个月里受物价部门干预，销售单价不得高于80元，要想在全部收回装修投资的基础上使第二个月的利润至少达到1700元，那么第二个月时里应该确定销售单价在什么范围内？
