题目内容
【题目】点A,B的坐标分别为(-2,3)和(1,3),抛物线y=ax2+bx+c(a<0)的 顶点在线段AB上运动时,形状保持不变,且与x轴交于C,D两点(C在D的左侧),给出下列结论:①c<3;②当x<-3时,y随x的增大而增大;③若点D的横坐标最大值为5,则点C的横坐标最小值为-5;④当四边形ACDB为平行四边形时,a=![]() .其中正确的是( )
.其中正确的是( )
A. ②④ B. ②③ C. ①③④ D. ①②④
【答案】A
【解析】∵点A,B的坐标分别为(2,3)和(1,3),
∴线段AB与y轴的交点坐标为(0,3),
又∵抛物线的顶点在线段AB上运动,抛物线与y轴的交点坐标为(0,c),
∴c3,(顶点在y轴上时取“=”),故①错误;
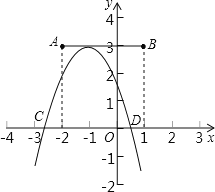
∵抛物线的顶点在线段AB上运动,
∴当x<2时,y随x的增大而增大,
因此,当x<3时,y随x的增大而增大,故②正确;
若点D的横坐标最大值为5,则此时对称轴为直线x=1,
根据二次函数的对称性,点C的横坐标最小值为24=6,故③错误;
根据顶点坐标公式, ![]() =3,
=3,
令y=0,则ax +bx+c=0,
CD =(![]() ) 4×
) 4×![]() =
=![]() ,
,
根据顶点坐标公式, ![]() =3,
=3,
∴![]() =12,
=12,
∴CD=![]() ×(12)=
×(12)= ![]() ,
,
∵四边形ACDB为平行四边形,
∴CD=AB=1(2)=3,
∴![]() =3=9,
=3=9,
解得a=![]() ,故④正确;
,故④正确;
综上所述,正确的结论有②④.
故选A.

练习册系列答案
相关题目
【题目】(6分)小聪是个数学爱好者,他发现从1开始,连续几个奇数相加,和的变化规律如右表所示:
加数个数 | 连续奇数的和S |
1 | 1= |
2 | 1+3=22 |
3 | 1+3+5=32 |
4 | 1+3+5+7=42 |
5 | 1+3+5+7+9=52 |
n | … |
(1)如果n=7,则S的值为 ;
(2)求1+3+5+7+…+199的值;
(3)求13+15+17+…+79的值.