题目内容
【题目】在平面直角坐标系中，我们把横、纵坐标均为整数的点叫做整点．已知反比例函数y=
（m＜0）与y=x2﹣4在第四象限内围成的封闭图形（包括边界）内的整点的个数为2，则实数m的取值范围为__．
【答案】﹣2≤m＜﹣1．
【解析】
根据题意可知抛物线在第四象限内的部分，然后根据反比例函数y=
（m＜0）与y=x2﹣4在第四象限内围成的封闭图形（包括边界）内的整点的个数为2，可以得到不等式组，从而可以求得m的取值范围．
∵y=x2﹣4，
∴当x=0时，y=﹣4，当y=0时，x=±2，当x=1时，y=﹣3，
∴抛物线y=x2﹣4在第四象限内的部分是（0，﹣4）到（2，0）这一段曲线部分，
∵反比例函数y=（m＜0）与y=x2﹣4在第四象限内围成的封闭图形（包括边界）内的整点的个数为2，
∴
，
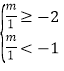解得，﹣2≤m＜﹣1，
故答案为：﹣2≤m＜﹣1.
练习册系列答案
相关题目
