��Ŀ����
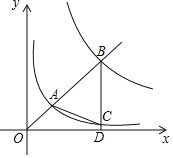
����Ŀ����֪�ף����������г����־���P�س������ﳵǰ����P��60ǧ��Q�أ��������ֳ�����1.5Сʱ����ʱ�ף��������������6ǧ�ף�������ֽӵ��������ʼ���Q�غ�������ԭ·����P�ؼף����������־�P�ص�·��y��ǧ�ף���ʱ��x��ʱ���ĺ���ͼ����ͼ��ʾ������������O��A��B��C��D��ʵ�ߣ���ʾ�ף�����O��E��F��G�����ߣ���ʾ�ң�
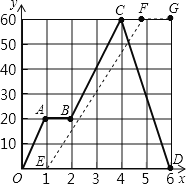
��1����������·��ͣ���� ��Сʱ���״�Q�ط���P��ʱ���ﳵ�ٶ�Ϊ�� ��ǧ��/ʱ��
��2�����Ҵ�P�ص�Q���ﳵ�����У����߶�EF����P�ص�·��y��ǧ�ף���ʱ��x��ʱ���ĺ�����ϵʽ���Ա���x��ȡֵ��Χ��
��3���������ֳ��������ڼף�����������ǰ����ʱ��x��ʱ����ֵΪ����ʱ���ף������������8ǧ�ף�
���𰸡���1��1Сʱ��30ǧ��/ʱ����2��y=24x��24��1��x��3.5������3��x=![]()
��������
��1������������ͼ���ɣ�
��2������ҵ��ٶȣ������ô���ϵ������ɣ�
��3�����ݣ�2���Ľ����з��̽�ɣ�
��1����ͼ���֪����������·��ͣ��1Сʱ���״�Q�ط���P��ʱ���ﳵ�ٶ�Ϊ��60����6��4��=30��ǧ��/ʱ����
�ʴ�Ϊ��1��30��
��2���״�P�ص�Q�ص��ٶ�Ϊ20��ǧ��/ʱ���������ҵ��ٶ�Ϊ����6+1.5��20����1.5=24��ǧ��/ʱ����
60��24=2.5��Сʱ����
���Ҵ�P�ص�Q���ﳵ�����У����߶�EF����P�ص�·��y��ǧ�ף���ʱ��x��ʱ���ĺ�����ϵʽΪy=24x+b����
24+b=0�����b=��24��
���Ҵ�P�ص�Q���ﳵ�����У����߶�EF����P�ص�·��y��ǧ�ף���ʱ��x��ʱ���ĺ�����ϵʽΪy=24x��24��1��x��3.5����
��3����������ã�
30��x��4��+��24x��24��=60��8��
���x=![]() ��
��
������������ǰ����ʱ��x=![]() ʱ���ף������������8ǧ�ף�
ʱ���ף������������8ǧ�ף�